Bài tập Câu 2 trang 223 SGK Đại số và Giải tích 11 Nâng cao là một bài toán quan trọng trong chương trình học. Bài toán này yêu cầu học sinh vận dụng kiến thức về hàm số, đạo hàm để giải quyết.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và kỹ năng giải bài tập.
Giải phương trình
Đề bài
Giải phương trình
\(\tan x = \cot 2x\)
Biểu diễn các nghiệm trên đường tròn lượng giác.
Lời giải chi tiết
Điều kiện
\(\left\{ \begin{array}{l}\cos x \ne 0\\\sin 2x = 2\sin x\cos x \ne 0\end{array} \right.\)
\( \Leftrightarrow \left\{ {\matrix{ {\sin x \ne 0} \cr {\cos x \ne 0} \cr } } \right. \Leftrightarrow x \ne k{\pi \over 2}\)
\(\eqalign{ & \tan x = \cot 2x \Leftrightarrow {{\sin x} \over {\cos x}} = {{\cos 2x} \over {\sin 2x}} \cr& \Rightarrow\cos x \cos 2x - \sin x\sin 2x = 0 \cr & \Leftrightarrow \cos 3x = 0 \cr & \Leftrightarrow 4{\cos ^3}x - 3\cos x = 0\cr &\Leftrightarrow \cos x\left( {4{{\cos }^2}x - 3} \right) = 0 \cr & \Leftrightarrow {\cos ^2}x = {3 \over 4} (do\, \cos x\ne 0) \cr & \Leftrightarrow {{1 + \cos 2x} \over 2} = {3 \over 4} \Leftrightarrow \cos 2x = {1 \over 2} \cr & \Leftrightarrow x =\pm {\pi \over 6} + k\pi (k\in\mathbb Z) \cr} \)
Biểu diễn nghiệm trên đường tròn được 4 điểm.
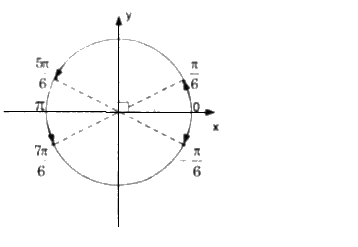
Cách khác:
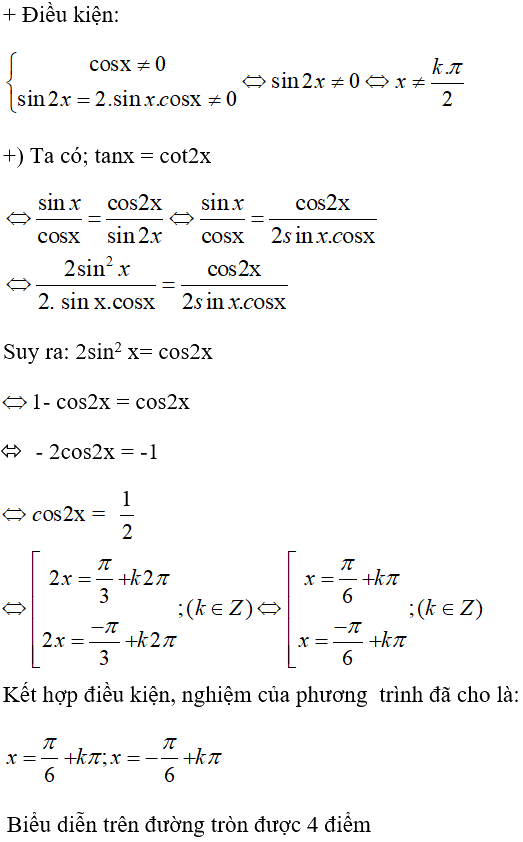
Bài tập Câu 2 trang 223 SGK Đại số và Giải tích 11 Nâng cao thuộc chương trình học lớp 11 nâng cao, tập trung vào việc ứng dụng các kiến thức về đạo hàm để giải quyết các bài toán thực tế. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản về đạo hàm, quy tắc tính đạo hàm và các ứng dụng của đạo hàm trong việc tìm cực trị, khoảng đơn điệu của hàm số.
Trước khi bắt đầu giải bài tập, điều quan trọng là phải đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Trong trường hợp của Câu 2 trang 223, học sinh cần xác định hàm số được cho, các điều kiện ràng buộc và mục tiêu cần đạt được (ví dụ: tìm cực trị, giải phương trình, chứng minh bất đẳng thức).
Để giải Câu 2 trang 223, chúng ta có thể thực hiện theo các bước sau:
Giả sử hàm số được cho là f(x) = x^3 - 3x^2 + 2. Chúng ta sẽ áp dụng các bước trên để giải bài tập:
Khi giải các bài tập về đạo hàm, học sinh cần chú ý các điểm sau:
Việc giải quyết thành công Câu 2 trang 223 SGK Đại số và Giải tích 11 Nâng cao không chỉ giúp học sinh củng cố kiến thức về đạo hàm mà còn rèn luyện kỹ năng giải quyết vấn đề, tư duy logic và khả năng áp dụng kiến thức vào thực tế. Những kỹ năng này rất quan trọng trong quá trình học tập và làm việc sau này.
Để hiểu sâu hơn về đạo hàm và các ứng dụng của nó, học sinh có thể tham khảo thêm các tài liệu sau:
Hy vọng với lời giải chi tiết và phân tích kỹ lưỡng này, các em học sinh sẽ hiểu rõ hơn về Câu 2 trang 223 SGK Đại số và Giải tích 11 Nâng cao và tự tin giải quyết các bài tập tương tự.