Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập trong sách giáo khoa Hình học 11 Nâng cao. Bài viết này sẽ tập trung vào việc giải Câu 9 trang 50 SGK Hình học 11 Nâng cao, giúp bạn hiểu rõ phương pháp và cách tiếp cận để giải quyết các bài toán tương tự.
Chúng tôi cam kết mang đến cho bạn những giải pháp học tập hiệu quả và dễ hiểu nhất, hỗ trợ bạn trong quá trình chinh phục môn Hình học.
Cho ba đường thẳng a, b, c không cùng nằm trong một mặt phẳng sao cho chúng đôi một cắt nhau. Chứng minh rằng chúng đồng quy
Đề bài
Cho ba đường thẳng a, b, c không cùng nằm trong một mặt phẳng sao cho chúng đôi một cắt nhau. Chứng minh rằng chúng đồng quy
Lời giải chi tiết
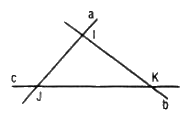
Gọi \(I =a\cap b\) \( \Rightarrow \left\{ \begin{array}{l}I \in {a}\\I \in {b}\end{array} \right.\)
Ta chứng minh \(I ∈ c\). Thật vậy,
Gọi (β) là mặt phẳng chứa hai đường thẳng cắt nhau \(a,c\).
\((\gamma)\) là mặt phẳng chứa hai đường thẳng cắt nhau \(b,c\).
Do ba đường thẳng không cùng nằm trong một mặt phẳng nên (β) và \((\gamma)\) phân biệt.
Ngoài ra
\(\left\{ \begin{array}{l}{c} \subset \left( \beta \right)\\{c} \subset \left( \gamma \right)\end{array} \right. \Rightarrow \left( \beta \right) \cap \left( \gamma \right) = {c}\)
\(I ∈ a\subset \left( \beta \right) \Rightarrow I ∈ (β) = (a,c)\)
\(I ∈ b\subset \left( \gamma \right) \Rightarrow I ∈ (\gamma) = (b,c)\)
Từ đó suy ra, \(I ∈(\beta ) \cap (\gamma )=c\).
Cách khác:
Gọi \(\left( P \right)\) là mặt phẳng chứa hai đường thẳng cắt nhau \(b\) và \(c\).
Gọi
\(\begin{array}{l}I = a \cap b \Rightarrow I \in b \subset \left( P \right)\\J = a \cap c \Rightarrow J \in c \subset \left( P \right)\end{array}\)
Nếu \(I,J\) phân biệt thì \(a\) đi qua cả \(I\) và \(J\) hay \(a \equiv IJ \subset \left( P \right)\)
Do đó \(a,b,c\) cùng nằm trong \(\left( P \right)\) (mâu thuẫn)
Do đó \(I \equiv J\) là điểm thuộc cả \(a,b,c\).
Vậy \(a,b,c\) đồng qui.
Câu 9 trang 50 SGK Hình học 11 Nâng cao thường liên quan đến các kiến thức về vectơ, đặc biệt là các phép toán vectơ trong không gian. Để giải quyết bài toán này một cách hiệu quả, chúng ta cần nắm vững các khái niệm cơ bản như vectơ, phép cộng, phép trừ vectơ, phép nhân vectơ với một số thực, và tích vô hướng của hai vectơ.
Trước khi đi vào giải chi tiết, hãy cùng ôn lại một số lý thuyết quan trọng:
Để giải Câu 9 trang 50, bước đầu tiên là đọc kỹ đề bài, xác định rõ các yếu tố đã cho và yêu cầu của bài toán. Sau đó, chúng ta cần lập kế hoạch giải cụ thể, bao gồm:
(Giả sử đề bài Câu 9 trang 50 là: Cho hai vectơ a và b có độ dài lần lượt là 3 và 4, và góc giữa chúng là 60 độ. Tính tích vô hướng a.b.)
Lời giải:
Áp dụng công thức tính tích vô hướng của hai vectơ, ta có:
a.b = |a||b|cos(θ) = 3 * 4 * cos(60°) = 12 * 0.5 = 6
Vậy, tích vô hướng của hai vectơ a và b là 6.
Ngoài Câu 9 trang 50, SGK Hình học 11 Nâng cao còn nhiều bài tập tương tự liên quan đến vectơ. Một số dạng bài tập phổ biến bao gồm:
Để giải các bài tập này, bạn cần nắm vững các kiến thức về vectơ, các phép toán vectơ, và tích vô hướng. Ngoài ra, việc vẽ hình minh họa và phân tích đề bài một cách cẩn thận cũng rất quan trọng.
Để củng cố kiến thức và kỹ năng giải bài tập, bạn nên luyện tập thêm với các bài tập khác trong SGK và các tài liệu tham khảo. Bạn cũng có thể tìm kiếm các bài tập trực tuyến trên giaitoan.edu.vn để thử thách bản thân.
Câu 9 trang 50 SGK Hình học 11 Nâng cao là một bài tập điển hình về ứng dụng của vectơ trong không gian. Việc nắm vững lý thuyết và phương pháp giải sẽ giúp bạn tự tin giải quyết các bài toán tương tự. Hãy luyện tập thường xuyên để nâng cao kỹ năng và kiến thức của mình.
Giaitoan.edu.vn hy vọng bài giải chi tiết này sẽ giúp bạn hiểu rõ hơn về Câu 9 trang 50 SGK Hình học 11 Nâng cao. Chúc bạn học tập tốt!