Bài toán này thường yêu cầu học sinh vận dụng kiến thức về vectơ, các phép toán vectơ, và mối quan hệ giữa các vectơ để giải quyết các vấn đề liên quan đến hình học không gian.
giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và kỹ năng giải toán.
Vẽ hình biểu diễn của một lục giác đều
Đề bài
Vẽ hình biểu diễn của một lục giác đều
Lời giải chi tiết
Xét hình lục giác đều ABCDEF, ta thấy:
Tứ giác OABC là hình thoi.
Các điểm D, E, F lần lượt là các điểm đối xứng của các điểm A, B, C qua tâm O.
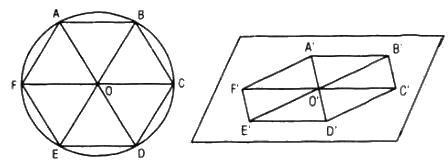
Từ đó ta suy ra cách vẽ hình biểu diễn của lục giác đều ABCDEF như sau:
- Vẽ hình bình hành O’A’B’C’ biểu diễn cho hình thoi OABC.
- Lấy các điểm D’, E’, F’ lần lượt đối xứng với các điểm A’, B’, C’ qua O’, ta được hình biểu diễn A’B’C’D’E’F’ của hình lục giác đều ABCDEF.
Bài toán Câu 46 trang 75 SGK Hình học 11 Nâng cao thường xoay quanh việc chứng minh các đẳng thức vectơ, xác định mối quan hệ giữa các điểm trong không gian, hoặc tính toán các yếu tố hình học dựa trên các vectơ đã cho. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản về vectơ, bao gồm:
Để cung cấp một lời giải cụ thể, chúng ta cần biết nội dung chính xác của bài toán. Tuy nhiên, dưới đây là một ví dụ về cách tiếp cận và giải quyết một bài toán tương tự:
Cho hình hộp ABCD.A'B'C'D'. Gọi M là trung điểm của cạnh AB. Chứng minh rằng: overrightarrow{AM} = 1/2overrightarrow{AB}.
Lời giải:
Ngoài bài toán chứng minh đẳng thức vectơ, Câu 46 trang 75 SGK Hình học 11 Nâng cao có thể xuất hiện các dạng bài tập khác, như:
Để giải quyết các dạng bài tập này, học sinh cần:
Dưới đây là một số mẹo giúp bạn giải toán Hình học 11 Nâng cao hiệu quả hơn:
Câu 46 trang 75 SGK Hình học 11 Nâng cao là một bài toán quan trọng giúp học sinh củng cố kiến thức về vectơ và ứng dụng của vectơ trong hình học không gian. Bằng cách nắm vững các kiến thức cơ bản, luyện tập thường xuyên và áp dụng các mẹo giải toán hiệu quả, bạn có thể tự tin giải quyết bài toán này và các bài toán tương tự.