Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số, đạo hàm để giải quyết các vấn đề thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin làm bài.
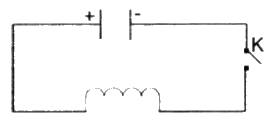
Cho mạch điện như hình 5.7.
Đề bài
Cho mạch điện như hình 5.7. Lúc đầu tụ điện có điện tích Q0. Khi đóng khóa K, tụ điện phóng điện qua cuộn dây ; điện tích q của tụ điện phụ thuộc vào thời gian t theo công thức \(q\left( t \right) = {Q_0}\sin \omega t.\) Trong đó, ω là tốc độ góc. Biết rằng cường độ I(t) của dòng điện tại thời điểm t được tính theo công thức \(I\left( t \right) = q'\left( t \right)\) Cho biết \({Q_0} = {10^{ - 8}}\,\text{ và }\,\omega = {10^6}\pi \,rad/s.\) Hãy tính cường độ của dòng điện tại thời điểm t = 6s (tính chính xác đến 10-5 mA)
Lời giải chi tiết
Cường độ dòng điện tại thời điểm t là :
\(I\left( t \right) = q'\left( t \right) = {Q_0}\omega \cos \omega t\)
Khi \({Q_0} = {10^{ - 8}}C\,\text{ và }\,\omega = {10^6}\pi \,rad/s\) thì cường độ dòng điện tại thời điểm t = 6s là :
\(I\left( 6 \right) = {10^{ - 8}}{.10^6}\pi .\cos \left( {{{10}^6}\pi .6} \right) \) \(= {\pi \over {100}}\left( A \right) \approx 31,41593\,\left( {mA} \right)\)
Câu 37 trang 212 SGK Đại số và Giải tích 11 Nâng cao thường xoay quanh các bài toán liên quan đến việc khảo sát hàm số bậc ba, hàm số đa thức, hoặc các bài toán ứng dụng đạo hàm để tìm cực trị, giá trị lớn nhất, giá trị nhỏ nhất của hàm số. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản về:
Để cung cấp một lời giải cụ thể, chúng ta cần biết chính xác nội dung của câu 37. Tuy nhiên, dựa trên kinh nghiệm giảng dạy và phân tích các đề thi, chúng ta có thể đưa ra một phương pháp giải tổng quát cho các bài toán tương tự:
Giả sử câu 37 yêu cầu khảo sát hàm số y = x3 - 3x2 + 2. Chúng ta sẽ thực hiện các bước sau:
Để học tốt môn Đại số và Giải tích 11 Nâng cao, bạn nên:
Câu 37 trang 212 SGK Đại số và Giải tích 11 Nâng cao là một bài tập điển hình để rèn luyện kỹ năng khảo sát hàm số và ứng dụng đạo hàm. Bằng cách nắm vững kiến thức cơ bản, luyện tập thường xuyên, và sử dụng các phương pháp giải hiệu quả, bạn có thể tự tin giải quyết bài toán này và đạt kết quả tốt trong môn học.