Chào mừng bạn đến với bài giải chi tiết Bài 11 trang 169 Toán 7 tập 1 trên giaitoan.edu.vn. Bài viết này sẽ cung cấp đáp án chính xác và phương pháp giải bài tập một cách dễ hiểu, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng cao, hỗ trợ tối đa cho học sinh trong việc chinh phục môn Toán.
Giải bài tập a) Tính độ cao của con diều so với mặt đất (h.18a).
Đề bài
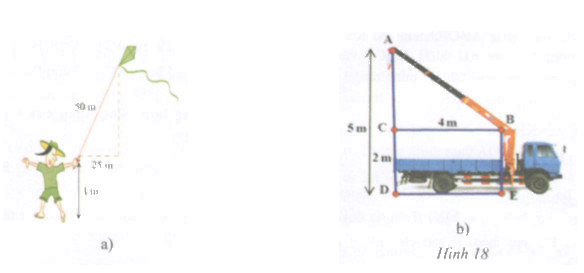
a) Tính độ cao của con diều so với mặt đất (h.18a).
b) Tính chiều dài cần cẩu AB (h.18b).
Lời giải chi tiết
a)Gọi độ cao của con diều so với tay người thả là h (m).
Áp dụng định lý Pythagore trong tam giác vuông ta có: \({h^2} + {25^2} = {50^2}.\)
\(\Rightarrow {h^2} = {50^2} - {25^2} = 2500 - 625 = 1875\)
Mà h > 0 do đó \(h = \sqrt {1875} \approx 43,3 (m)\)
Độ cao của con diều so với mặt đất là: \(43,3 + 1 = 44,3 (m).\)
b) \(AC = AD - CD = 5 - 2 = 3(m)\)
Áp dụng định lý Pythagore cho tam giác ABC vuông tại C ta có: \(A{B^2} = A{C^2} + B{C^2}\)
Do đó: \(A{B^2} = {3^2} + {4^2} = 9 + 16 = 25\)
Mà AB > 0 nên \(AB = \sqrt {25} = 5(m).\) Vậy chiều dài của cần cẩu là 5m.
Bài 11 trang 169 Toán 7 tập 1 thuộc chương trình học Toán 7, tập trung vào việc vận dụng các kiến thức đã học về biểu thức đại số để giải các bài toán thực tế. Bài tập này thường yêu cầu học sinh phải hiểu rõ các quy tắc về dấu ngoặc, thứ tự thực hiện các phép tính, và các tính chất của phép cộng, trừ, nhân, chia.
Bài 11 thường bao gồm các dạng bài tập sau:
Để giải Bài 11 trang 169 Toán 7 tập 1 một cách hiệu quả, bạn cần:
Ví dụ: Tính giá trị của biểu thức 3x + 2y khi x = 2 và y = -1.
Giải:
Thay x = 2 và y = -1 vào biểu thức, ta có:
3x + 2y = 3(2) + 2(-1) = 6 - 2 = 4
Vậy, giá trị của biểu thức 3x + 2y khi x = 2 và y = -1 là 4.
Ngoài sách giáo khoa, bạn có thể tham khảo thêm các tài liệu sau để học Bài 11 trang 169 Toán 7 tập 1:
Bài 11 trang 169 Toán 7 tập 1 là một bài tập quan trọng giúp học sinh củng cố kiến thức về biểu thức đại số. Bằng cách nắm vững các quy tắc và tính chất, cùng với việc luyện tập thường xuyên, bạn sẽ có thể giải bài tập một cách dễ dàng và tự tin.