Chào mừng bạn đến với bài giải chi tiết Bài 7 trang 169 Toán 7 tập 1 tại giaitoan.edu.vn. Chúng tôi cung cấp đáp án chính xác và phương pháp giải bài tập một cách dễ hiểu, giúp bạn nắm vững kiến thức và tự tin hơn trong học tập.
Bài viết này sẽ hướng dẫn bạn từng bước giải quyết các bài toán trong Bài 7, đồng thời cung cấp các kiến thức nền tảng cần thiết để bạn hiểu rõ bản chất của vấn đề.
Giải bài tập Cho tam giác ABC vuông tại A có
Đề bài
Cho tam giác ABC vuông tại A có \(\widehat C = {60^0}\) . Kẻ AH vuông goác với BC tại H, trên tia đối của tia AH lấy điểm D sao cho HD = HA.
a) Chứng minh rằng \(\Delta ABD\) đều.
b) Từ D kẻ đường thẳng song song với AB cắt BC tại M. Chứng minh rằng đều.
Lời giải chi tiết
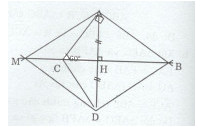
a)Ta có: \(\widehat {ACH} + \widehat {HAC} = {90^0}(\Delta AHC\) vuông tại H)
\(\widehat {HAC} + \widehat {HAB} = {90^0}(\Delta ABC\) vuông tại A)
Suy ra: \(\widehat {ACB} = \widehat {HAB} = {60^0}\)
Mặt khác \(AH \bot BC(gt) \Rightarrow \widehat {AHB} = \widehat {DHB} = \widehat {MHA} = \widehat {MHD} = {90^0}\)
Xét tam giác ABH và DBH có:
AH = DH (giả thiết)
HB là cạnh chung.
\(\widehat {AHB} = \widehat {DHB}({90^0})\)
Do đó: \(\Delta ABH = \Delta DBH(c.g.c)\)
Suy ra: AB = BD => tam giác ABD cân tại B.
Mà \(\widehat {BAD} = {60^0}.\) Do vậy tam giác ABD đều.
b) Ta có: AB // MD (gt)
\(\Rightarrow \widehat {ADM} = \widehat {BAD}\) (hai góc so le trong) nên \(\widehat {ADM} = {60^0}.\)
Xét tam giác MHA và MHD có:
HA = HD (gt)
\(\widehat {MHA} = \widehat {MHD}( = {90^0})\)
MH là cạnh chung.
Do đó: \(\Delta MHA = \Delta MHD(c.g.c) \Rightarrow MA = MD \Rightarrow \Delta ADM\) cân tại M.
Mà \(\widehat {ADM} = {60^0}.\) Vậy tam giác ADM đều.
Bài 7 trang 169 Toán 7 tập 1 thuộc chương trình học Toán 7, tập trung vào việc ôn tập và củng cố các kiến thức đã học về biểu thức đại số, đơn thức, đa thức. Bài tập trong bài này thường yêu cầu học sinh vận dụng các quy tắc cộng, trừ, nhân, chia đơn thức, đa thức để rút gọn biểu thức, tìm giá trị của biểu thức tại một giá trị cụ thể của biến, hoặc chứng minh đẳng thức.
Bài 7 thường bao gồm các dạng bài tập sau:
Đây là dạng bài tập cơ bản nhất, yêu cầu học sinh sử dụng các quy tắc cộng, trừ, nhân, chia đơn thức, đa thức để đưa biểu thức về dạng đơn giản nhất. Ví dụ:
Rút gọn biểu thức: 3x + 2y - x + 5y
Giải:
3x + 2y - x + 5y = (3x - x) + (2y + 5y) = 2x + 7y
Dạng bài tập này yêu cầu học sinh thay giá trị của biến vào biểu thức và thực hiện các phép tính để tìm ra giá trị của biểu thức. Ví dụ:
Tính giá trị của biểu thức 2x + 3y khi x = 1 và y = -1
Giải:
2x + 3y = 2(1) + 3(-1) = 2 - 3 = -1
Đây là dạng bài tập nâng cao hơn, yêu cầu học sinh biến đổi một vế của đẳng thức để đưa về dạng tương đương với vế còn lại. Ví dụ:
Chứng minh rằng: (a + b)2 = a2 + 2ab + b2
Giải:
(a + b)2 = (a + b)(a + b) = a(a + b) + b(a + b) = a2 + ab + ba + b2 = a2 + 2ab + b2
Để giải Bài 7 trang 169 Toán 7 tập 1 một cách hiệu quả, bạn cần:
Bài tập: Rút gọn biểu thức: 5x2 - 3x + 2x2 + x - 1
Giải:
5x2 - 3x + 2x2 + x - 1 = (5x2 + 2x2) + (-3x + x) - 1 = 7x2 - 2x - 1
Khi giải Bài 7 trang 169 Toán 7 tập 1, bạn cần chú ý:
Bài 7 trang 169 Toán 7 tập 1 là một bài tập quan trọng giúp học sinh củng cố kiến thức về biểu thức đại số. Bằng cách nắm vững các quy tắc và phương pháp giải, bạn có thể tự tin giải quyết các bài tập trong bài và đạt kết quả tốt trong học tập. Chúc bạn học tốt!