Chào mừng các em học sinh đến với lời giải Bài tập 9 trang 121 Toán 7 tập 2. Bài tập này thuộc chương trình học Toán 7, tập trung vào việc rèn luyện kỹ năng giải toán về các phép toán với số hữu tỉ.
Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập tương tự.
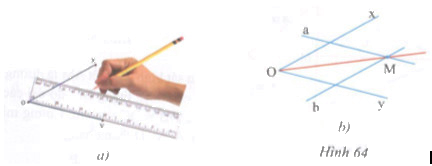
Giải bài tập Hình 64 giới thiệu cách vẽ tia phân giác của góc xOy bằng thước thẳng (hai lề).
Đề bài
Hình 64 giới thiệu cách vẽ tia phân giác của góc xOy bằng thước thẳng (hai lề).
- Áp một lề của thước vào cạnh Oy, kẻ đường thẳng a theo lề kia (hình 64a).
- Làm tương tự với cạnh Ox, ta kẻ đường thẳng b.
- Gọi M là giao điểm của a và b, ta có OM là tia phân giác của xOy (hình 64b). Chứng minh OM là tia phân giác của góc xOy.
Lời giải chi tiết
Khoảng cách từ điểm M đến Ox và khoảng cách từ điểm M đến Oy đều là khoảng cách giữa hai lề song song của thước kẻ nên chúng bằng nhau.
Theo định lí đảo của “tính chất tia phân giác của một góc” ta có điểm M nằm trên tia phân giác của góc xOy. Vậy OM là tia phân giác của góc xOy.
Bài tập 9 trang 121 Toán 7 tập 2 yêu cầu học sinh thực hiện các phép tính với số hữu tỉ, bao gồm cộng, trừ, nhân, chia. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các quy tắc về phép toán với số hữu tỉ, đặc biệt là quy tắc dấu và quy tắc chuyển đổi phân số.
Phần a của bài tập thường yêu cầu học sinh tính giá trị của một biểu thức chứa các số hữu tỉ. Để làm được điều này, học sinh cần thực hiện các phép tính theo đúng thứ tự ưu tiên: trong ngoặc trước, nhân chia trước, cộng trừ sau.
Ví dụ, nếu biểu thức là: (1/2 + 1/3) * 2/5, học sinh cần thực hiện các bước sau:
Phần b của bài tập thường yêu cầu học sinh tìm giá trị của x trong một phương trình chứa số hữu tỉ. Để giải phương trình này, học sinh cần sử dụng các phép biến đổi tương đương để đưa phương trình về dạng x = một số hữu tỉ.
Ví dụ, nếu phương trình là: x + 1/2 = 3/4, học sinh cần thực hiện các bước sau:
Bài tập: Tính giá trị của biểu thức: (2/3 - 1/2) : 5/6
Giải:
Kết luận: Giá trị của biểu thức là 1/5.
Để rèn luyện thêm kỹ năng giải bài tập về số hữu tỉ, học sinh có thể tham khảo các bài tập tương tự sau:
Bài tập 9 trang 121 Toán 7 tập 2 là một bài tập quan trọng giúp học sinh củng cố kiến thức về các phép toán với số hữu tỉ. Bằng cách nắm vững các quy tắc và thực hành thường xuyên, học sinh có thể tự tin giải các bài tập tương tự và đạt kết quả tốt trong môn Toán.
Hy vọng với lời giải chi tiết và hướng dẫn cụ thể này, các em học sinh sẽ hiểu rõ hơn về bài tập và có thể tự giải thành công. Chúc các em học tập tốt!