Bài tập 34 trang 98 thuộc chương trình Toán 7 tập 2, tập trung vào việc rèn luyện kỹ năng giải toán về các phép toán với số hữu tỉ. Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Chúng tôi không chỉ cung cấp đáp án mà còn phân tích từng bước giải, giúp học sinh hiểu rõ phương pháp và cách tiếp cận bài toán.
Giải bài tập Cho tam giác ABC vuông tại A có M là trung điểm của AC. Gọi E và F lần lượt là hình chiếu kẻ từ A và C đến các đường thẳng BM.
Đề bài
Cho tam giác ABC vuông tại A có M là trung điểm của AC. Gọi E và F lần lượt là hình chiếu kẻ từ A và C đến các đường thẳng BM.
Chứng minh: \(AB < {{BE + BF} \over 2} < BC\)
Lời giải chi tiết
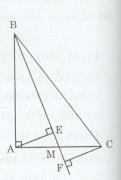
Xét ∆AEM vuông tại E và ∆MCF vuông tại F ta có:
AM = MC (M là trung điểm của AC)
Và \(\widehat {EMA} = \widehat {CMF}\) (hai góc đối đỉnh)
Do đó: ∆AEM = ∆CFM (cạnh huyền – góc nhọn)
=> EM = MF
BE + BF = BE + BM + MF = BE + BM + EM (vì MF = EM)
= (BE + EM) + BM = BM + BM = 2BM
Do đó \(BM = {{BE + BF} \over 2}(1)\)
Mà \(BA \bot AC\) tại A,
Mặt khác, ta có AM < AC => BM < BC (3)
Từ (1), (2) và (3) ta có: \(AB < {{BE + BF} \over 2} < BC.\)
Bài tập 34 trang 98 Toán 7 tập 2 là một phần quan trọng trong chương trình học Toán 7, giúp học sinh củng cố kiến thức về các phép toán với số hữu tỉ. Dưới đây là giải chi tiết từng bài tập, kèm theo phân tích phương pháp giải để học sinh hiểu rõ hơn.
a) (1/2 + 1/3) * 6/5
Lời giải:
b) 2/5 : (1/3 - 1/5)
Lời giải:
a) x + 2/5 = 1/2
Lời giải:
b) x - 1/3 = 3/4
Lời giải:
Lời giải:
Trong quá trình giải các bài tập về số hữu tỉ, học sinh cần nắm vững các quy tắc sau:
Để học tốt môn Toán 7, học sinh cần thường xuyên luyện tập và ôn tập kiến thức. Giaitoan.edu.vn cung cấp đầy đủ các bài giải, bài tập và tài liệu học tập để hỗ trợ học sinh trong quá trình học tập.
Ngoài bài tập 34 trang 98, học sinh có thể tham khảo thêm các bài tập khác trong sách giáo khoa Toán 7 tập 2 để củng cố kiến thức. Bên cạnh đó, học sinh cũng có thể tìm hiểu thêm về các ứng dụng của số hữu tỉ trong thực tế.
| Ứng dụng | Ví dụ |
|---|---|
| Đo lường | Đo chiều dài, chiều rộng, diện tích, thể tích,... |
| Tính toán tiền bạc | Tính giá cả, chi phí, lợi nhuận,... |
| Khoa học | Tính toán các đại lượng vật lý, hóa học,... |
Hy vọng với bài giải chi tiết và phân tích phương pháp giải trên, học sinh sẽ hiểu rõ hơn về bài tập 34 trang 98 Toán 7 tập 2 và tự tin giải các bài tập tương tự. Chúc các em học tốt!