Giải Toán 7 Bài 8 Trang 169 - giaitoan.edu.vn

Bài 8 trang 169 Tài liệu dạy – học Toán 7 tập 1

Bài 8 trang 169 Toán 7: Giải bài tập chi tiết

Bài 8 trang 169 thuộc Tài liệu dạy – học Toán 7 tập 1 là một phần quan trọng trong chương trình học Toán 7. Bài học này tập trung vào việc rèn luyện kỹ năng giải toán về các biểu thức đại số đơn giản.

Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho từng bài tập trong Bài 8, giúp học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.

Giải bài tập Cho tam giác DEF cân tại D. Gọi H là trung điểm của EF.

Đề bài

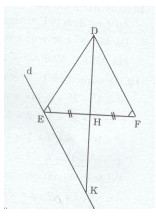
Cho tam giác DEF cân tại D. Gọi H là trung điểm của EF.

a) Chứng minh rằng DH là phân giác của \(\widehat {EDF}.\)

b) Từ E kẻ đường thẳng d song song với DF, d cắt đường thẳng DH tại K. Chứng minh rằng tam giác DEK cân.

Lời giải chi tiết

Bài 8 trang 169 Tài liệu dạy – học Toán 7 tập 1 1

a)Xét tam giác DEH và DFH ta có:

DH là cạnh chung.

DE = DF (tam giác DEF cân tại D)

HE = HF (H là trung điểm của EF)

Do đó: \(\eqalign{ & \Delta DEH = \Delta DFH(c.c.c) \cr & \Rightarrow \widehat {EDH} = \widehat {FDH} \cr} \)

Vậy DH là tia phân giác của góc EDF.

b) Ta có: \(\widehat {EKD} = \widehat {FDH}\) (so le trong và EK // DF)

Mà \(\widehat {EDK} = \widehat {FDH}(cmt)\)

Do đó: \(\widehat {EKD} = \widehat {EDK}\)

Vậy tam giác DEK cân tại E.\)AB = \sqrt {11} \)

Khai phá tiềm năng Toán lớp 7 của bạn! Đừng bỏ lỡ Bài 8 trang 169 Tài liệu dạy – học Toán 7 tập 1 tại chuyên mục toán 7 trên học toán. Với bộ bài tập toán trung học cơ sở được biên soạn chuyên sâu, cập nhật chính xác theo chương trình sách giáo khoa, các em sẽ tự tin ôn luyện, củng cố kiến thức vững chắc và nâng cao khả năng tư duy. Phương pháp học trực quan, sinh động sẽ mang lại hiệu quả học tập vượt trội mà bạn hằng mong muốn!

Bài 8 trang 169 Toán 7: Giải chi tiết và hướng dẫn

Bài 8 trang 169 Toán 7 tập 1 yêu cầu học sinh vận dụng các kiến thức đã học về biểu thức đại số, các phép toán với biểu thức đại số để giải các bài tập cụ thể. Dưới đây là lời giải chi tiết cho từng bài tập, kèm theo hướng dẫn giải để học sinh hiểu rõ phương pháp và tự tin áp dụng vào các bài tập tương tự.

Bài 8.1 trang 169 Toán 7

Đề bài: Tính giá trị của biểu thức: 3x + 5y khi x = 2 và y = -1.

Lời giải:

Thay x = 2 và y = -1 vào biểu thức 3x + 5y, ta được:
3 * 2 + 5 * (-1) = 6 - 5 = 1
Vậy, giá trị của biểu thức 3x + 5y khi x = 2 và y = -1 là 1.

Bài 8.2 trang 169 Toán 7

Đề bài: Tính giá trị của biểu thức: a² - 2ab + b² khi a = -3 và b = 2.

Lời giải:

Thay a = -3 và b = 2 vào biểu thức a² - 2ab + b², ta được:
(-3)² - 2 * (-3) * 2 + 2² = 9 + 12 + 4 = 25
Vậy, giá trị của biểu thức a² - 2ab + b² khi a = -3 và b = 2 là 25.

Bài 8.3 trang 169 Toán 7

Đề bài: Tìm giá trị của x để biểu thức: 2x - 4 = 0.

Lời giải:

Chuyển -4 sang vế phải, ta được: 2x = 4
Chia cả hai vế cho 2, ta được: x = 2
Vậy, giá trị của x để biểu thức 2x - 4 = 0 là x = 2.

Bài 8.4 trang 169 Toán 7

Đề bài: Tìm giá trị của y để biểu thức: 5y + 10 = 0.

Lời giải:

Chuyển 10 sang vế phải, ta được: 5y = -10
Chia cả hai vế cho 5, ta được: y = -2
Vậy, giá trị của y để biểu thức 5y + 10 = 0 là y = -2.

Bài 8.5 trang 169 Toán 7

Đề bài: Rút gọn biểu thức: 3x + 2x - 5x.

Lời giải:

3x + 2x - 5x = (3 + 2 - 5)x = 0x = 0
Vậy, biểu thức 3x + 2x - 5x được rút gọn thành 0.

Bài 8.6 trang 169 Toán 7

Đề bài: Rút gọn biểu thức: 4y - y + 3y.

Lời giải:

4y - y + 3y = (4 - 1 + 3)y = 6y
Vậy, biểu thức 4y - y + 3y được rút gọn thành 6y.

Lưu ý khi giải bài tập Toán 7 Bài 8

Luôn thay đúng giá trị của biến vào biểu thức.
Thực hiện các phép toán theo đúng thứ tự ưu tiên (nhân, chia trước; cộng, trừ sau).
Kiểm tra lại kết quả sau khi giải xong.

Tài liệu tham khảo thêm

Để nắm vững kiến thức về biểu thức đại số và các phép toán với biểu thức đại số, học sinh có thể tham khảo thêm các tài liệu sau:

Sách giáo khoa Toán 7 tập 1
Sách bài tập Toán 7 tập 1
Các trang web học Toán online uy tín như giaitoan.edu.vn

Hy vọng với lời giải chi tiết và hướng dẫn giải trên, các em học sinh sẽ tự tin hơn khi giải các bài tập trong Bài 8 trang 169 Toán 7 tập 1. Chúc các em học tốt!