Chào mừng bạn đến với bài giải Bài 5 trang 171 Toán 7 tập 1 tại giaitoan.edu.vn. Bài viết này cung cấp lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng cao, hỗ trợ tối đa cho quá trình học tập của các em. Hãy cùng bắt đầu với bài giải Bài 5 trang 171 Toán 7 tập 1 ngay bây giờ!
Giải bài tập Cho tam giác ABC cân tại A có
Đề bài
Cho tam giác ABC cân tại A có \(\widehat B = 2\widehat A.\) Phân giác của góc B cắt AC tại D.
a) Tính số đo các góc của tam giác ABC.
b) Chứng minh rằng DA = DB.
c) Chứng minh rằng DA = BC.
Lời giải chi tiết
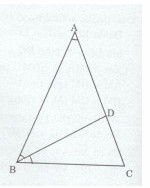
a)Ta có:
\(\widehat {ABC} = \widehat {ACB}(\Delta ABC\) cân tại A)
\(\widehat {ABC} = 2\widehat {BAC}(gt)\)
Nên \(\widehat {ACB} = 2\widehat {BAC}\)
Mà tam giác ABC có: \(\widehat {BAC} + \widehat {ABC} + \widehat {ACB} = {180^0}.\)
Do đó: \(\eqalign{ & \widehat {BAC} + 2\widehat {BAC} + 2\widehat {BAC} = {180^0} \cr & \Rightarrow 5\widehat {BAC} = {180^0} \Rightarrow \widehat {BAC} = {{{{180}^0}} \over 5} = {36^0} \cr} \)
Do đó: \(\widehat {ABC} = \widehat {ACB} = {2.36^0} = {72^0}.\)
b) Ta có: \(\widehat {BAD} = {{\widehat {ABC}} \over 2}(gt)\)
\(\widehat {ABD} = \widehat {DBC} = {{\widehat {ABC}} \over 2}\) (BD là tia phân giác của ABC)
Do đó: \(\widehat {BAD} = \widehat {ABD} = \widehat {DBC}.\)
Tam giác ADB có: \(\widehat {DAB} = \widehat {ABD} \Rightarrow \Delta ADB\) cân tại D.
Vậy DA = DB.
c) Ta có: \(\widehat {BDC} = \widehat {ABD} + \widehat {DAB}\) (góc ngoài của tam giác ABD)
Mà \(\widehat {ABD} = \widehat {DAB}\) nên \(\widehat {BDC} = 2\widehat {BAD}\)
\(\widehat {ABC} = \widehat {ACB} = 2\widehat {BAD}(\Delta ABC\) cân tại A và \(\widehat B = 2\widehat A)\)
Suy ra: \(\widehat {BDC} = \widehat {DCB} \Rightarrow \Delta BDC\) cân tại B => BD = BC.
Mà AD = BD (chứng minh trên). Do đó: BC = AD.
Bài 5 trang 171 Toán 7 tập 1 thuộc chương trình học Toán 7, tập trung vào việc vận dụng các kiến thức đã học về biểu thức đại số để giải các bài toán thực tế. Bài tập này thường yêu cầu học sinh phải hiểu rõ các quy tắc về dấu ngoặc, thứ tự thực hiện các phép tính, và các tính chất của phép cộng, trừ, nhân, chia.
Bài 5 thường bao gồm các dạng bài tập sau:
Để giải Bài 5 trang 171 một cách hiệu quả, học sinh cần:
Ví dụ 1: Tính giá trị của biểu thức 3x + 2y khi x = 2 và y = -1.
Giải:
3x + 2y = 3 * 2 + 2 * (-1) = 6 - 2 = 4
Ví dụ 2: Rút gọn biểu thức 2(x + y) - (x - y).
Giải:
2(x + y) - (x - y) = 2x + 2y - x + y = (2x - x) + (2y + y) = x + 3y
Khi giải Bài 5 trang 171, học sinh cần chú ý:
Để hiểu rõ hơn về các kiến thức liên quan đến Bài 5 trang 171, học sinh có thể tham khảo thêm:
Để rèn luyện kỹ năng giải Bài 5 trang 171, học sinh có thể tự giải các bài tập sau:
Bài 5 trang 171 Toán 7 tập 1 là một bài tập quan trọng giúp học sinh củng cố kiến thức về biểu thức đại số. Bằng cách nắm vững các quy tắc và tính chất, cùng với việc luyện tập thường xuyên, các em sẽ có thể giải quyết các bài toán tương tự một cách dễ dàng và hiệu quả.