Bài tập 6 trang 127 thuộc chương trình Toán 7 tập 2, tập trung vào việc rèn luyện kỹ năng giải toán về các phép tính với số hữu tỉ. Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Chúng tôi hiểu rằng việc học Toán đôi khi có thể gặp nhiều khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn hướng dẫn giải bài tập 6 trang 127 một cách cẩn thận, đảm bảo tính chính xác và dễ tiếp thu.
Giải bài tập Cho tam giác ABC vuông tại A
Đề bài
Cho tam giác ABC vuông tại A, có \(AB = {1 \over 2}AC\) , AD là tia phân giác \(\widehat {BAC}\,\,\left( {D \in BC} \right)\), gọi E là trung điểm của AC.
a) Chứng minh rằng DE = DB.
b) AB cắt DE tại K. Chứng minh rằng \(\Delta DCK\) cân và B là trung điểm của đoạn thẳng AK.
c) AD cắt CK tại H. Chứng minh rằng \(AK \bot KC\)
d) Biết AB = 4 cm. Tính DK.
Lời giải chi tiết
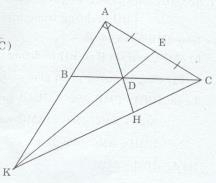
a) Xét ∆DEA và ∆DBA ta có:
AD là cạnh chung,
\(\widehat {DAE} = \widehat {BAD}\) (AD là tia phân giác của \(\widehat {BAC}\))
\(AE = AB( = {1 \over 2}AC)\)
Do đó: ∆DEA = ∆DBA (c.g.c) => DE = DB
b) Ta có: \(\widehat {ABD} + \widehat {KBD} = 180^\circ\) (kề bù),
\(\widehat {AED} + \widehat {CED} = 180^\circ\) (kề bù)
\(\widehat {ABD} = \widehat {AED}\) (∆DBA = ∆DEA)
Do đó \(\widehat {KBD} = \widehat {CED}.\)
Xét ∆KBD = ∆CED (g.c.g) => KD = CD => Tam giác DCK cân tại D.
Ta có: AB = EC (\( = {1 \over 2}AC\))
BK = EC (∆KBD = ∆CED)
Suy ra AB = BK. Vậy B là trung điểm của AK (\(B \in AK\)).
c) Ta có: \(AB = {1 \over 2}AC(gt)\)
\(AB = {1 \over 2}AK\) (B là trung điểm của AK)
Do đó AC = AK => ∆AKC cân tại A.
Mà AH là đường phân giác của ∆AKC.
Nên AH cũng là đường cao của ∆AKC. Vậy \(AH \bot KC.\)
d) \(AB = {1 \over 2}AC(gt)\)
=> AC = 2AB = 2.4 = 8 (cm)
∆ABC vuông tại A có BC2 = AB2 + AC2 (định lí Pythagore)
=> BC2 = 42 + 82 = 80 \( \Rightarrow BC = 4\sqrt 5 (cm)\)
∆AKC có KE là đường trung tuyến (E là trung điểm của AC), CB là đường trung tuyến (B là trung điểm của AK và KE cắt CB tại D)
Nên D là trọng tâm của ∆AKC \( \Rightarrow DC = {2 \over 3}BC = {2 \over 3}.4\sqrt 5 = {{8\sqrt 5 } \over 3}(cm)\)
Mà DK = DC (câu b). Do đó \(DK = {{8\sqrt 5 } \over 3}(cm).\)
Bài tập 6 trang 127 Toán 7 tập 2 là một phần quan trọng trong chương trình học Toán 7, giúp học sinh củng cố kiến thức về các phép tính với số hữu tỉ, đặc biệt là phép cộng, trừ, nhân, chia số hữu tỉ. Để giải quyết bài tập này một cách hiệu quả, học sinh cần nắm vững các quy tắc và tính chất cơ bản của các phép toán này.
Bài tập 6 thường bao gồm các dạng bài tập sau:
Để giải bài tập 6 trang 127 một cách chính xác, học sinh cần thực hiện theo các bước sau:
Ví dụ 1: Tính giá trị của biểu thức sau:
(1/2) + (2/3) - (1/4)
Giải:
Để tính giá trị của biểu thức này, ta cần tìm mẫu số chung của các phân số. Mẫu số chung nhỏ nhất của 2, 3 và 4 là 12. Do đó, ta quy đồng các phân số như sau:
(1/2) = (6/12)
(2/3) = (8/12)
(1/4) = (3/12)
Thay các phân số đã quy đồng vào biểu thức ban đầu, ta có:
(6/12) + (8/12) - (3/12) = (6 + 8 - 3)/12 = 11/12
Vậy, giá trị của biểu thức là 11/12.
Ví dụ 2: Tìm x trong phương trình sau:
x + (1/3) = (5/6)
Giải:
Để tìm x, ta cần chuyển (1/3) sang vế phải của phương trình:
x = (5/6) - (1/3)
Quy đồng mẫu số của các phân số, ta có:
(1/3) = (2/6)
Thay phân số đã quy đồng vào phương trình, ta có:
x = (5/6) - (2/6) = (5 - 2)/6 = 3/6 = 1/2
Vậy, x = 1/2.
Ngoài sách giáo khoa, học sinh có thể tham khảo các tài liệu sau để học tập và luyện tập:
Bài tập 6 trang 127 Toán 7 tập 2 là một bài tập quan trọng giúp học sinh củng cố kiến thức về các phép tính với số hữu tỉ. Bằng cách nắm vững các quy tắc và tính chất cơ bản, cùng với việc luyện tập thường xuyên, học sinh có thể tự tin giải quyết các bài tập tương tự và đạt kết quả tốt trong môn Toán.