Chào mừng các em học sinh đến với lời giải Bài tập 2 trang 130 Toán 7 tập 2. Bài tập này thuộc chương trình học Toán 7, tập trung vào việc rèn luyện kỹ năng giải toán về các phép toán với số hữu tỉ.
Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và phương pháp giải bài tập hiệu quả.
Giải bài tập Cho tam giác DEF vuông tại D có cạnh DE = 12 cm, cạnh DF = 16 cm.
Đề bài
Cho tam giác DEF vuông tại D có cạnh DE = 12 cm, cạnh DF = 16 cm.
Trên cạnh DF lấy điểm A sao cho DA = DE (A nằm giữa D và F). Trên tia đối của tia ED lấy điểm B sao cho DB = DF (E nằm giữa D và B). Kẻ DH là đường cao của tam giác DEF. Đường thẳng DH cắt AB tại P.
a) Tính độ dài cạnh EF
b) Chứng minh \(\Delta DEF = \Delta DAB\)
c) Chứng minh DP là trung tuyến của tam giác DAB.
Lời giải chi tiết
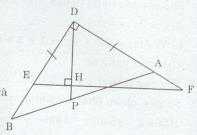
a) ∆DEF vuông tại D
Ta có EF2 = DE2 + DF2 (định lí Pythagore)
=> EF2 = 122 + 162 = 400 = 202
=> EF = 20 (cm).
b) Xét ∆DEF và ∆DAB ta có: DE = DA (gt)
\(\widehat D\) (chung)
DF = DB (gt)
Do đó: ∆DEF = ∆DAB (c.g.c).
c) Ta có: \(\widehat {DEF} + \widehat F = 90^\circ\) (∆DEF vuông tại D) và \(\widehat {PDA} + \widehat F = 90^\circ\) (∆DHF vuông tại H)
\( \Rightarrow \widehat {DEF} = \widehat {PDA}\)
Mà \(\widehat {DEF} = \widehat {DAP}\) (∆DEF = ∆DAB). Nên \(\widehat {PDA} = \widehat {DAP}\)
=> ∆DPA cân tại P
Vậy PD = PA (1)
Ta có: \(\widehat {DFE} + \widehat {DEF} = 90^\circ\) (∆DEF vuông tại D)
\(\widehat {BDP} = \widehat {DEF} = 90^\circ\) (∆DEH vuông tại H)
\( \Rightarrow \widehat {DFE} = \widehat {BDP}\)
Mà \(\widehat {DFE} = \widehat {DBP}\) (∆DEF = ∆DAB). Nên \(\widehat {BDP} = \widehat {DBP}\)
=> ∆DBP cân tại P => PA = BP
=> P là trung điểm của AB (\(P \in AB\))
Vậy DP là đường trung tuyến của tam giác DAB.
Bài tập 2 trang 130 Toán 7 tập 2 là một bài tập quan trọng trong chương trình học Toán 7, tập trung vào việc vận dụng các kiến thức về số hữu tỉ, các phép toán cộng, trừ, nhân, chia số hữu tỉ để giải quyết các bài toán thực tế.
(Đề bài cụ thể của Bài tập 2 trang 130 sẽ được trình bày tại đây. Ví dụ: Tính: a) 1/2 + 1/3; b) 2/5 - 1/4; c) 3/7 * 2/9; d) 4/5 : 1/2)
Để giải bài tập này, chúng ta cần nắm vững các quy tắc sau:
a) Tính 1/2 + 1/3
Áp dụng quy tắc cộng hai phân số, ta có:
1/2 + 1/3 = (1 * 3 + 1 * 2) / (2 * 3) = (3 + 2) / 6 = 5/6
b) Tính 2/5 - 1/4
Áp dụng quy tắc trừ hai phân số, ta có:
2/5 - 1/4 = (2 * 4 - 1 * 5) / (5 * 4) = (8 - 5) / 20 = 3/20
c) Tính 3/7 * 2/9
Áp dụng quy tắc nhân hai phân số, ta có:
3/7 * 2/9 = (3 * 2) / (7 * 9) = 6 / 63 = 2/21
d) Tính 4/5 : 1/2
Áp dụng quy tắc chia hai phân số, ta có:
4/5 : 1/2 = 4/5 * 2/1 = (4 * 2) / (5 * 1) = 8/5
Bài tập này giúp học sinh củng cố kiến thức về các phép toán với số hữu tỉ. Để làm tốt bài tập này, học sinh cần:
Ngoài ra, học sinh có thể tham khảo thêm các bài tập tương tự trong sách giáo khoa và các tài liệu tham khảo khác để nâng cao kỹ năng giải toán.
Để luyện tập thêm, các em có thể thử giải các bài tập sau:
Bài tập 2 trang 130 Toán 7 tập 2 là một bài tập cơ bản nhưng quan trọng trong chương trình học Toán 7. Việc nắm vững kiến thức và kỹ năng giải bài tập này sẽ giúp học sinh tự tin hơn trong việc giải quyết các bài toán phức tạp hơn.
Giaitoan.edu.vn hy vọng rằng lời giải chi tiết và phân tích này sẽ giúp các em học sinh hiểu rõ hơn về bài tập và đạt kết quả tốt trong học tập.