Giải Bài tập 27 trang 98 Toán 7 tập 2

Bài tập 27 trang 98 Tài liệu dạy – học Toán 7 tập 2

Bài tập 27 trang 98 Toán 7 tập 2: Hướng dẫn giải chi tiết

Chào mừng các em học sinh đến với lời giải Bài tập 27 trang 98 Toán 7 tập 2. Bài tập này thuộc chương trình học Toán 7, tập trung vào việc rèn luyện kỹ năng giải toán về các biểu thức đại số và các phép toán cơ bản.

Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập tương tự.

Giải bài tập Góc đáy của tam giác cân nhỏ hơn 60o. Hãy cho biết cạnh đáy hay cạnh bên của tam giác cân là lớn nhất, vì sao ?

Đề bài

Góc đáy của tam giác cân nhỏ hơn 60^o. Hãy cho biết cạnh đáy hay cạnh bên của tam giác cân là lớn nhất, vì sao ?

Lời giải chi tiết

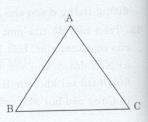
Bài tập 27 trang 98 Tài liệu dạy – học Toán 7 tập 2 1

∆ABC cân tại A nên \(\widehat B = {{180^\circ - \widehat A} \over 2}\)

Mà \(\widehat B < 60^\circ\). Nên

\(\eqalign{ & {{180^\circ - \widehat A} \over 2} < 60^\circ \cr & 180^\circ - \widehat A < 2.60^\circ \cr & 180^\circ - \widehat A < 120^\circ \cr & \Rightarrow \widehat A > 180^\circ - 120^\circ \Rightarrow \widehat A > 60^\circ \cr}\)

Do đó \(\widehat A > \widehat B = \widehat C\)

∆ABC có \(\widehat A > \widehat B = \widehat C\) => BC > AC = AB

Vậy cạnh đáy của tam giác cân là lớn nhất.

Khai phá tiềm năng Toán lớp 7 của bạn! Đừng bỏ lỡ Bài tập 27 trang 98 Tài liệu dạy – học Toán 7 tập 2 tại chuyên mục giải bài tập toán 7 trên soạn toán. Với bộ bài tập toán trung học cơ sở được biên soạn chuyên sâu, cập nhật chính xác theo chương trình sách giáo khoa, các em sẽ tự tin ôn luyện, củng cố kiến thức vững chắc và nâng cao khả năng tư duy. Phương pháp học trực quan, sinh động sẽ mang lại hiệu quả học tập vượt trội mà bạn hằng mong muốn!

Bài tập 27 trang 98 Toán 7 tập 2: Giải chi tiết và phương pháp

Bài tập 27 trang 98 Toán 7 tập 2 là một bài tập quan trọng trong chương trình học Toán 7, tập trung vào việc vận dụng các kiến thức đã học về biểu thức đại số, các phép toán cộng, trừ, nhân, chia số hữu tỉ để giải quyết các bài toán thực tế. Dưới đây là lời giải chi tiết và phương pháp giải bài tập này:

Đề bài:

Cho các biểu thức sau:

A = x + 2y
B = 2x - y
C = x² + y²

Tính giá trị của A, B, C khi x = 1, y = -2.

Lời giải:

Để tính giá trị của A, B, C khi x = 1, y = -2, ta thay trực tiếp giá trị của x và y vào các biểu thức:

A = x + 2y = 1 + 2*(-2) = 1 - 4 = -3
B = 2x - y = 2*1 - (-2) = 2 + 2 = 4
C = x² + y² = 1² + (-2)² = 1 + 4 = 5

Vậy, khi x = 1, y = -2, ta có:

A = -3
B = 4
C = 5

Phương pháp giải:

Bài tập này yêu cầu học sinh vận dụng kiến thức về:

Biểu thức đại số: Hiểu rõ khái niệm biểu thức đại số và cách thay giá trị của biến vào biểu thức.
Các phép toán cộng, trừ, nhân, chia số hữu tỉ: Thực hiện chính xác các phép toán này để tính giá trị của biểu thức.
Thứ tự thực hiện các phép toán: Tuân thủ đúng thứ tự thực hiện các phép toán (nhân, chia trước; cộng, trừ sau).

Bài tập tương tự và luyện tập

Để củng cố kiến thức và kỹ năng giải bài tập về biểu thức đại số, các em có thể tham khảo và giải các bài tập tương tự sau:

Tính giá trị của biểu thức P = 3x - 5y khi x = -1, y = 2.
Tính giá trị của biểu thức Q = x² - 2xy + y² khi x = 3, y = -1.
Tính giá trị của biểu thức R = (x + y)(x - y) khi x = 2, y = -3.

Lưu ý khi giải bài tập:

Đọc kỹ đề bài để hiểu rõ yêu cầu của bài toán.
Thay đúng giá trị của biến vào biểu thức.
Thực hiện các phép toán một cách cẩn thận và chính xác.
Kiểm tra lại kết quả sau khi giải xong.

Tài liệu tham khảo thêm

Để học tốt môn Toán 7, các em có thể tham khảo thêm các tài liệu sau:

Sách giáo khoa Toán 7 tập 1 và tập 2.
Sách bài tập Toán 7.
Các trang web học Toán online uy tín như giaitoan.edu.vn.
Các video bài giảng Toán 7 trên YouTube.

Kết luận

Bài tập 27 trang 98 Toán 7 tập 2 là một bài tập cơ bản nhưng quan trọng trong chương trình học Toán 7. Việc nắm vững kiến thức và kỹ năng giải bài tập này sẽ giúp các em tự tin hơn trong việc học Toán và giải quyết các bài toán phức tạp hơn.