Chào mừng các em học sinh đến với lời giải Bài tập 9 trang 116 Toán 7 tập 1. Bài tập này thuộc chương trình học Toán 7, tập trung vào việc rèn luyện kỹ năng giải toán về các phép toán với số hữu tỉ.
Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và phương pháp giải bài tập hiệu quả.
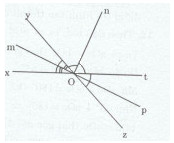
Giải bài tập Cho hai góc kề bù
Đề bài
Cho hai góc kề bù \(\widehat {xOy}\)và \(\widehat {yOt}\) . Gouj Om, On lần lượt là tia phân giác của \(\widehat {xOy}\) và \(\widehat {yOt}\).
a) Tính số đo \(\widehat {mOn}\)
b) Vẽ \(\widehat {tOz}\) là góc đối đỉnh của \(\widehat {xOy}\), vẽ tia Op là tia đối của tia Om. Chứng tỏ rằng Op, On lần lượt là tia phân giác của \(\widehat {tOz}\) và \(\widehat {mOp}\)
Lời giải chi tiết
a)Ta có: \(\widehat {xOy}\) và \(\widehat {yOt}\) là hai góc kề bù.
Nên \(\widehat {xOy} + \widehat {yOt} = {180^0}\)
Mà \(\widehat {mOy} = {1 \over 2}\widehat {xOy}\) (Om là tia phân giác của góc xOy)
Và \(\widehat {yOn} = {1 \over 2}\widehat {yOt}\) (On là tia phân giác của góc yOt)
Do đó:
\(\eqalign{ & \widehat {mOn} = \widehat {mOy} + \widehat {yOn} \cr & = {1 \over 2}\widehat {xOy} + {1 \over 2}\widehat {yOt} = {1 \over 2}(\widehat {xOy} + \widehat {yOt}) = {1 \over 2}{.180^0} = {90^0} \cr} \)
b) Ta có: \(\widehat {xOm} = \widehat {mOy}\) (Om là tia phân giác của \(\widehat {xOy})\)
\(\widehat {xOm} = \widehat {tOp}\) (hai góc đối đỉnh)
\(\widehat {mOy} = \widehat {pOz}\) (hai góc đối đỉnh)
Do đó: \(\widehat {tOP} = \widehat {pOz}.\) Vậy Op là tia phân giác của góc tOz
Ta cũng có: \(\widehat {yOm} = \widehat {tOp}\)
Mà \(\widehat {yOn} = \widehat {nOt}\) (On là tia phân giác góc yOt). Do đó \(\widehat {yOm} + \widehat {yOn} = \widehat {tOp} + \widehat {nOt}\)
Suy ra \(\widehat {mOn} = \widehat {pOn}.\) Vậy On là tia phân giác của góc mOp.
Bài tập 9 trang 116 Toán 7 tập 1 yêu cầu học sinh vận dụng kiến thức về các phép toán với số hữu tỉ để thực hiện các phép tính. Để giải bài tập này một cách chính xác, học sinh cần nắm vững các quy tắc cộng, trừ, nhân, chia số hữu tỉ, cũng như các tính chất giao hoán, kết hợp, phân phối của các phép toán này.
Trước khi bắt đầu giải bài tập, học sinh cần đọc kỹ đề bài để hiểu rõ yêu cầu. Xác định các số hữu tỉ cần thực hiện phép tính và các phép toán cần thực hiện. Chú ý đến dấu của các số hữu tỉ và thứ tự thực hiện các phép toán.
Để giải bài tập này, học sinh có thể áp dụng các phương pháp sau:
(Giả sử đề bài là: Thực hiện các phép tính sau: a) 1/2 + 1/3; b) 2/5 - 1/4; c) 3/7 * 2/5; d) 4/9 : 1/3)
Quy đồng mẫu số: 1/2 = 3/6; 1/3 = 2/6
Cộng hai phân số: 3/6 + 2/6 = 5/6
Vậy, 1/2 + 1/3 = 5/6
Quy đồng mẫu số: 2/5 = 8/20; 1/4 = 5/20
Trừ hai phân số: 8/20 - 5/20 = 3/20
Vậy, 2/5 - 1/4 = 3/20
Nhân hai phân số: (3 * 2) / (7 * 5) = 6/35
Vậy, 3/7 * 2/5 = 6/35
Tìm nghịch đảo của 1/3: 3/1
Nhân 4/9 với 3/1: (4 * 3) / (9 * 1) = 12/9 = 4/3
Vậy, 4/9 : 1/3 = 4/3
Để hiểu rõ hơn về cách giải bài tập về các phép toán với số hữu tỉ, học sinh có thể tham khảo các ví dụ minh họa sau:
Khi giải bài tập này, học sinh cần lưu ý những điều sau:
Kiến thức về số hữu tỉ có ứng dụng rộng rãi trong thực tế, ví dụ như:
Bài tập 9 trang 116 Toán 7 tập 1 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải toán về các phép toán với số hữu tỉ. Hy vọng với lời giải chi tiết và phân tích trên, các em học sinh sẽ hiểu rõ hơn về bài tập này và có thể giải các bài tập tương tự một cách dễ dàng.