Chào mừng các em học sinh đến với lời giải Bài tập 1 trang 151 Toán 7 tập 1. Bài tập này thuộc chương trình học Toán 7, tập trung vào việc rèn luyện kỹ năng giải toán về các phép toán với số hữu tỉ.
Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập tương tự. Hãy cùng chúng tôi khám phá lời giải ngay sau đây!
Giải bài tập Tìm số đo x, y ở các hình 37a, b, c, d, e, f
Đề bài
Tìm số đo x, y ở các hình 37a, b, c, d, e, f
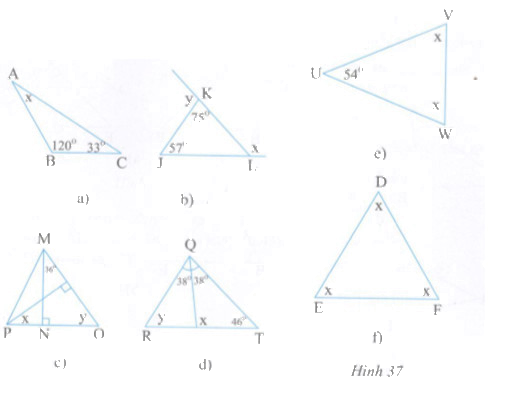
Phương pháp giải - Xem chi tiết
- Tổng 3 góc trong tam giác bằng \(180^{0}\)
- Góc ngoài tam gíac bằng tổng 2 góc trong không kề với nó
Lời giải chi tiết
a)Tam giác ABC có: \(\widehat A + \widehat B + \widehat C = {180^0}\)
Do đó: \(x + {120^0} + {33^0} = {180^0} \Rightarrow x = {180^0} - {120^0} - {33^0} = {27^0}\)
b) \(y + {75^0} = {180^0}\) (hai góc kề bù) \( \Rightarrow x = {75^0} + {57^0} = {132^0}\)
\(x = \widehat {JKL} + \widehat {KJL}\) (góc ngoài của tam giác KJL)
\(\rightarrow x = {75^0} + {57^0} = {132^0}\)
c) Tam giác MNO có: \(\widehat {MNO} + \widehat {NMO} + \widehat {MON} = {180^0}\)
Do đó: \({90^0} + {36^0} + \widehat {MON} = {180^0} \)
\(\Rightarrow \widehat {MON} = y = {180^0} - {90^0} - {36^0} = {54^0}\)
\(x + {90^0} + y = {180^0}\) (tổng ba góc trong một tam giác)
\(\Rightarrow x = {180^0} - {90^0} - {54^0} = {36^0}\)
d) Tam giác RQT có: \(\widehat {RQT} + \widehat {QTR} + \widehat {QRT} = {180^0}\)
Do đó: \({38^0} + {38^0} + {46^0} + y = {180^0} \)
\(\Rightarrow y = {180^0} - {38^0} - {38^0} - {46^0} = {58^0}\)
\(x = y + {38^0}\) (góc ngoài của tam giác) \( \Rightarrow x = {58^0} + {38^0} = {96^0}\)
e) Tam giác UVW có:\(\widehat U + \widehat V + \widehat {\rm{W}} = {180^0}\)
Do đó: \({54^0} + x + x = {180^0} \Rightarrow 2x = {180^0} - {54^0} = {126^0}\)
\(\Rightarrow x = {{{{126}^0}} \over 2} = {63^0}\)
f) Tam giác DEF có: \(\widehat D + \widehat E + \widehat F = {180^0}\)
Do đó: \(x + x + x = {180^0} \Leftrightarrow 3x = {180^0} \Rightarrow x = {{{{180}^0}} \over 3} = {60^0}\)
Bài tập 1 trang 151 Toán 7 tập 1 yêu cầu chúng ta thực hiện các phép tính với số hữu tỉ. Để giải bài tập này một cách chính xác, chúng ta cần nắm vững các quy tắc về cộng, trừ, nhân, chia số hữu tỉ. Dưới đây là lời giải chi tiết cho từng câu hỏi trong bài tập:
Để cộng hai phân số, chúng ta cần quy đồng mẫu số. Mẫu số chung nhỏ nhất của 2 và 3 là 6. Do đó, ta có:
(1/2) + (1/3) = (3/6) + (2/6) = (3+2)/6 = 5/6
Tương tự như câu a, chúng ta quy đồng mẫu số. Mẫu số chung nhỏ nhất của 5 và 4 là 20. Do đó, ta có:
(2/5) - (1/4) = (8/20) - (5/20) = (8-5)/20 = 3/20
Để nhân hai phân số, chúng ta nhân tử số với tử số và mẫu số với mẫu số:
(3/4) * (2/7) = (3*2)/(4*7) = 6/28 = 3/14
Để chia hai phân số, chúng ta nhân phân số thứ nhất với nghịch đảo của phân số thứ hai:
(5/6) : (1/2) = (5/6) * (2/1) = (5*2)/(6*1) = 10/6 = 5/3
Để củng cố kiến thức về các phép toán với số hữu tỉ, các em có thể tự giải thêm các bài tập tương tự. Ví dụ:
Kiến thức về số hữu tỉ có ứng dụng rất lớn trong đời sống hàng ngày, ví dụ như tính toán tiền bạc, đo lường, chia sẻ đồ vật,...
Bài tập 1 trang 151 Toán 7 tập 1 là một bài tập cơ bản nhưng quan trọng để nắm vững kiến thức về các phép toán với số hữu tỉ. Hy vọng với lời giải chi tiết và hướng dẫn trên, các em sẽ tự tin giải bài tập và đạt kết quả tốt trong môn Toán.
| Phép tính | Lời giải |
|---|---|
| (1/2) + (1/3) | 5/6 |
| (2/5) - (1/4) | 3/20 |
| (3/4) * (2/7) | 3/14 |
| (5/6) : (1/2) | 5/3 |