Bài 8 trang 171 Toán 7 tập 1 thuộc chương trình học Toán 7, tập trung vào việc luyện tập các kiến thức về biểu thức đại số. Bài tập này giúp học sinh củng cố kỹ năng biến đổi biểu thức, thực hiện các phép toán với biến và hiểu rõ hơn về ứng dụng của đại số trong giải quyết các bài toán thực tế.
Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu cho từng bài tập trong Bài 8, giúp học sinh tự học hiệu quả và đạt kết quả tốt nhất.
Giải bài tập Cho tam giác ABC nhọn (AB < AC). Kẻ AH vuông góc với BC tại H. Trên tia đối của tia HA lấy điểm M sao cho H là trung điểm của AM.
Đề bài
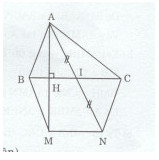
Cho tam giác ABC nhọn (AB < AC). Kẻ AH vuông góc với BC tại H. Trên tia đối của tia HA lấy điểm M sao cho H là trung điểm của AM.
a) Chứng minh rằng \(\Delta ABH = \Delta MBH.\)
b) Chứng minh rằng \(\widehat {BAC} = \widehat {BMC}.\)
c) Gọi I là trung điểm của BC. Trên tia đối của tia IA lấy điểm N sao cho I là trung điểm của AN. Chứng minh rằng NC = BM.
d) Cho AB = 13 cm, AH = 12 cm, HC = 16 cm. Tính độ dài của cạnh AC, BC.
Lời giải chi tiết
a)Xét hai tam giác ABH và MBH ta có:
\(\widehat {AHB} = \widehat {MHB}( = {90^0})\)
AH = MH (H là trung điểm của AM)
BH là cạnh chung.
Do đó: \(\Delta ABH = \Delta MBH(c.g.c)\)
b) Ta có: \(\Delta ABH = \Delta MBH\) (chứng minh câu a)
Suy ra: AB = MB và \(\widehat {ABH} = \widehat {MBH}.\)
Xét hai tam giác ABC và MBC ta có:
BC là cạnh chung
\(\widehat {ABC} = \widehat {MBC}(cmt)\)
AB = BM (chứng minh trên)
Do đó: \(\Delta ABC = \Delta MBC(c.g.c) \Rightarrow \widehat {BAC} = \widehat {BMC}.\)
c) Xét tam giác ABI và NCI ta có:
AI = NI (I là trung điểm của AN)
\(\widehat {AIB} = \widehat {CIN}\) (hai góc đối đỉnh)
BI = CI (I là trung điểm của BC)
Do đó: \(\Delta ABI = \Delta NCI(c.g.c) \Rightarrow AB = CN.\)
Mà AB = BM (chứng minh câu b) nên CN = BM.
d) Tam giác ABH vuông tại H \(\Rightarrow B{H^2} + A{H^2} = A{B^2}\) (định lí Pythagore)
\(B{H^2} = A{B^2} - A{H^2} = {13^2} - {12^2} = 169 - 144 = 25.\)
Mà BH > 0. Do đó: \(BH = \sqrt {25} = 5(cm).\)
Tam giác AHC vuông tại H \(\Rightarrow A{C^2} = A{H^2} + H{C^2}\) (định lí Pythagore)
Do đó: \(A{C^2} = A{H^2} + H{C^2} = {12^2} + {16^2} = 400.\)
Mà AC > 0 nên \(AC = \sqrt {400} = 20(cm)\)
Mặt khác BC = BH + HC = 5 + 16 = 21 (cm).
Bài 8 trang 171 Toán 7 tập 1 là một phần quan trọng trong chương trình học Toán 7, giúp học sinh rèn luyện kỹ năng biến đổi biểu thức đại số. Dưới đây là giải chi tiết từng bài tập, kèm theo hướng dẫn để học sinh có thể tự giải và hiểu rõ hơn về kiến thức.
a) 3x + 5y - 2x + y
Giải:
3x + 5y - 2x + y = (3x - 2x) + (5y + y) = x + 6y
b) 7a2 - 4a + 3a2 + 2a
Giải:
7a2 - 4a + 3a2 + 2a = (7a2 + 3a2) + (-4a + 2a) = 10a2 - 2a
a) 2x - 3y khi x = 5 và y = -2
Giải:
2x - 3y = 2(5) - 3(-2) = 10 + 6 = 16
b) a2 + 2ab - b2 khi a = 1 và b = -1
Giải:
a2 + 2ab - b2 = (1)2 + 2(1)(-1) - (-1)2 = 1 - 2 - 1 = -2
a) Tổng của x và y
Biểu thức: x + y
b) Hiệu của a và b
Biểu thức: a - b
c) Tích của 3 và x
Biểu thức: 3x
a) 5x2 - 2x + 1 khi x = 0
Giải:
5x2 - 2x + 1 = 5(0)2 - 2(0) + 1 = 0 - 0 + 1 = 1
b) 3y3 + 2y2 - y + 5 khi y = 1
Giải:
3y3 + 2y2 - y + 5 = 3(1)3 + 2(1)2 - (1) + 5 = 3 + 2 - 1 + 5 = 9
a) x + 5 = 12
Giải:
x = 12 - 5 = 7
b) 2x - 3 = 7
Giải:
2x = 7 + 3 = 10
x = 10 / 2 = 5
Một khu vườn hình chữ nhật có chiều dài là 10m và chiều rộng là 5m. Hãy viết biểu thức tính chu vi của khu vườn đó.
Giải:
Chu vi của khu vườn hình chữ nhật là: 2(chiều dài + chiều rộng) = 2(10 + 5) = 2(15) = 30m
Bài 8 trang 171 Toán 7 tập 1 cung cấp một nền tảng vững chắc cho học sinh trong việc hiểu và vận dụng các kiến thức về biểu thức đại số. Việc luyện tập thường xuyên và nắm vững các quy tắc biến đổi biểu thức sẽ giúp học sinh giải quyết các bài toán một cách nhanh chóng và chính xác.
Giaitoan.edu.vn luôn đồng hành cùng học sinh trên con đường chinh phục môn Toán. Hãy truy cập website để xem thêm các bài giải và tài liệu học tập hữu ích khác.