Chào mừng các em học sinh đến với lời giải Bài tập 13 trang 122 Toán 7 tập 2. Bài tập này thuộc chương trình học Toán 7, tập trung vào việc rèn luyện kỹ năng giải toán về các phép toán với số hữu tỉ.
Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án và cách giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập tương tự.
Giải bài tập Cho tam giác ABC cân tại A. Tia phân giác của góc B và C gặp nhau tại M. Tia AM cắt BC tại H. Chứng minh rằng H là trung điểm của BC.
Đề bài
Cho tam giác ABC cân tại A. Tia phân giác của góc B và C gặp nhau tại M. Tia AM cắt BC tại H. Chứng minh rằng H là trung điểm của BC.
Lời giải chi tiết
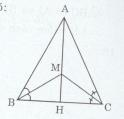
∆ABC có M là giao điểm của hai đường phân giác xuất phát từ B và C (gt)
Nên theo định lý về ba đường phân giác của tam giác, ta có:
M là điểm cách đều ba cạnh của tam giác ABC.
=> AM là tia phân giác của \(\widehat {BAC}\)
∆ABC cân tại A có AH là đường phân giác
=> AH cũng là đường trung tuyến
Vậy H là trung điểm của BC.
Bài tập 13 trang 122 Toán 7 tập 2 là một phần quan trọng trong chương trình học Toán 7, tập trung vào việc củng cố kiến thức về các phép toán với số hữu tỉ. Để giúp các em học sinh hiểu rõ hơn và giải quyết bài tập một cách hiệu quả, chúng tôi xin trình bày lời giải chi tiết và hướng dẫn từng bước.
Bài tập 13 bao gồm các câu hỏi liên quan đến việc thực hiện các phép cộng, trừ, nhân, chia số hữu tỉ. Các em cần vận dụng các quy tắc về dấu của số hữu tỉ, quy tắc chuyển vế, và các tính chất của phép toán để giải quyết bài tập.
Để giải bài tập 13 trang 122 Toán 7 tập 2, các em cần thực hiện theo các bước sau:
Ví dụ 1: Tính giá trị của biểu thức sau:
(1/2) + (2/3) - (1/4)
Giải:
(1/2) + (2/3) - (1/4) = (6/12) + (8/12) - (3/12) = (6 + 8 - 3)/12 = 11/12
Ví dụ 2: Tìm x biết:
x + (1/3) = (5/6)
Giải:
x = (5/6) - (1/3) = (5/6) - (2/6) = 3/6 = 1/2
Số hữu tỉ là số có thể biểu diễn dưới dạng phân số a/b, trong đó a là số nguyên và b là số nguyên khác 0. Các số hữu tỉ bao gồm số nguyên, số phân số, và số thập phân hữu hạn hoặc vô hạn tuần hoàn.
Các phép toán với số hữu tỉ tuân theo các quy tắc sau:
Số hữu tỉ được ứng dụng rộng rãi trong thực tế, ví dụ như:
Bài tập 13 trang 122 Toán 7 tập 2 là một bài tập quan trọng giúp các em học sinh củng cố kiến thức về các phép toán với số hữu tỉ. Hy vọng với lời giải chi tiết và hướng dẫn từng bước, các em sẽ tự tin giải quyết bài tập một cách hiệu quả.
Chúc các em học tập tốt!