Chào mừng bạn đến với bài giải Bài 9 trang 171 Toán 7 tập 1 trên giaitoan.edu.vn. Chúng tôi cung cấp đáp án chi tiết và cách giải bài tập một cách dễ hiểu, giúp bạn nắm vững kiến thức và tự tin hơn trong học tập.
Bài 9 thuộc chương trình Toán 7 tập 1, tập trung vào việc rèn luyện kỹ năng giải toán và áp dụng các kiến thức đã học vào thực tế.
Giải bài tập Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm N sao cho BM = CN.
Đề bài
Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm N sao cho BM = CN.
a) Tam giác AMN là tam giác gì ? Vì sao ?
b) Kẻ \(BH \bot AM(H \in AM)\) kẻ \(CK \bot AN(K \in AN).\) Chứng minh rằng BH = CK. Tam giác OBC là tam giác gì ? Vì sao ?
Lời giải chi tiết
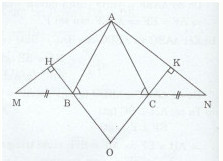
a)Ta có: \(\eqalign{ & \widehat {ABM} + \widehat {ABC} = {180^0} \cr & \widehat {ACN} + \widehat {ACB} = {180^0} \cr} \) (kề bù)
Suy ra \(\widehat {ABM} + \widehat {ACB} = \widehat {ACN} + \widehat {ACB}\)
Mà \(\widehat {ABC} = \widehat {ACB}(\Delta ABC\) cân tại A)
Nên \(\widehat {ABM} = \widehat {ACN}\)
Xét tam giác ABM và CAN ta có:
AB = AC (tam giác ABC cân tại A)
BM = CN (giả thiết)
\(\widehat {ABM} = \widehat {ACN}(cmt)\)
Do đó: \(\Delta ABM = \Delta ACN(c.g.c) \Rightarrow AM = AN.\)
Vậy tam giác AMN cân tại A.
b) Xét tam giác MBH vuông tại H và tam giác NCK vuông tại K ta có:
MB = CN (giả thiết)
\(\widehat {BMH} = \widehat {CNK}(\Delta AMN\) cân tại A)
Do đó: \(\Delta MBH = \Delta NCK\) (cạnh huyền - góc nhọn) => BH = CK.
c) Ta có: \(\eqalign{ & \widehat {MBH} = \widehat {OBC} \cr & \widehat {KCN} = \widehat {OCB} \cr} \) (hai góc đối đỉnh)
Mà \(\widehat {MBH} = \widehat {KCN}(\Delta MBH = \Delta NCK) \Rightarrow \widehat {OBC} = \widehat {OCB}\)
Vậy tam giác OBC cân tại O.
Bài 9 trang 171 Toán 7 tập 1 là một bài tập quan trọng trong chương trình học, yêu cầu học sinh vận dụng kiến thức về các phép toán cơ bản, đặc biệt là phép nhân và phép chia số hữu tỉ. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các quy tắc và tính chất của các phép toán này.
Bài 9 trang 171 Toán 7 tập 1 thường bao gồm các dạng bài tập sau:
Để giải Bài 9 trang 171 Toán 7 tập 1, bạn có thể làm theo các bước sau:
Ví dụ 1: Tính giá trị của biểu thức sau:
(2/3) * (4/5) + (1/2) * (3/4)
Giải:
(2/3) * (4/5) + (1/2) * (3/4) = 8/15 + 3/8 = (8*8 + 3*15) / (15*8) = (64 + 45) / 120 = 109/120
Ví dụ 2: Tìm x trong phương trình sau:
x * (2/5) = 3/10
Giải:
x = (3/10) / (2/5) = (3/10) * (5/2) = 15/20 = 3/4
Để học tốt hơn về Bài 9 trang 171 Toán 7 tập 1, bạn có thể tham khảo các tài liệu sau:
Bài 9 trang 171 Toán 7 tập 1 là một bài tập quan trọng trong chương trình học. Hy vọng rằng với hướng dẫn chi tiết và các ví dụ minh họa trên, bạn sẽ có thể giải bài tập này một cách dễ dàng và hiệu quả. Chúc bạn học tốt!
| Phép toán | Quy tắc |
|---|---|
| Nhân hai số hữu tỉ | (a/b) * (c/d) = (a*c) / (b*d) |
| Chia hai số hữu tỉ | (a/b) / (c/d) = (a/b) * (d/c) = (a*d) / (b*c) |