Chào mừng các em học sinh đến với lời giải Bài tập 13 trang 157 Toán 7 tập 1. Bài tập này thuộc chương trình học Toán 7, tập trung vào việc rèn luyện kỹ năng giải toán về các phép toán với số hữu tỉ.
Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập tương tự.
Giải bài tập Cho tam giác ABC vuông tại A, kẻ
Đề bài
Cho tam giác ABC vuông tại A, kẻ \(AH \bot BC(H \in BC)\) . Trên tia đối của tia HA ta lấy điểm M sao cho HM = HA.
a) Chứng minh rằng \(\Delta ABH = \Delta MBH\)
b) Gọi I là trung điểm của BC. Qua C kẻ đường thẳng vuông góc với AC, đường kẻ này cắt tia AI tại D. Chứng minh rằng AB = DC.
c) Chứng minh rằng \(\widehat {ACB} = \widehat {AMB}\)
d) Chứng minh rằng BC // DM.
Lời giải chi tiết
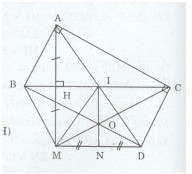
a)Xét tam giác AHB và MHB có:
HA = HM (giả thiết)
\(\widehat {AHB} = \widehat {MHB}( = {90^0})\)
BH là cạnh chung.
Dó đó: \(\Delta AHB = \Delta MHB(c.g.c).\)
b) Ta có: \(BA \bot AC\)(tam giác ABC vuông tại A) và \(DC \bot AC(gt)\)
\( \Rightarrow AB//CD \Rightarrow \widehat {ABI} = \widehat {DCI}\)
Xét tam giác ABI và DCI có:
\(\widehat {ABI} = \widehat {DCI}(cmt)\)
BI = CI (I là trung điểm của BC)
Và \(\widehat {AIB} = \widehat {DIC}\)(hai góc đối đỉnh)
Do đó: \(\Delta ABI = \Delta DCI(g.c.g)\)
Suy ra : AB = CD.
c) Ta có: \(\widehat {ACB} + \widehat {HAC} = {90^0}(\Delta AHC\)vuông tại H)
\(\eqalign{ & \widehat {BAH} + \widehat {HAC} = {90^0}(\widehat {BAC} = {90^0}) \cr & \Rightarrow \widehat {ACB} = \widehat {BAH} \cr} \)
Mà \(\widehat {BAH} = \widehat {BMH}(\Delta ABH = \Delta MBH)\) nên \(\widehat {ACB} = \widehat {AMB}\)
d) Cách 1:
Gọi O là giao điểm của BD và CM.
Xét tam giác MBC và DCB có:
BM = CD (=AB)
\(\widehat {MBC} = \widehat {DCB}( = \widehat {ABH})\)
BC là cạnh chung.
Do đó: \(\Delta MBC = \Delta DCB(c.g.c) \)
\(\Rightarrow \widehat {BCM} = \widehat {CBD} \)
\(\Rightarrow \widehat {BCM} = ({180^0} - \widehat {BOC}):2(1)\)
Xét tam giác BDM và CMD có:
\(BD = CM(\Delta MBC = \Delta DCB)\)
BM = CD
MD là cạnh chung.
Do đó: \(\Delta BDM = \Delta CMD(c.c.c) \)
\(\Rightarrow \widehat {BDM} = \widehat {CMD} \)
\(\Rightarrow \widehat {CMD} = ({180^0} - \widehat {MOD}):2(2)\)
Mà \(\widehat {BOC} = \widehat {MOD}(3)\) (đối đỉnh)
Từ (1), (2), (3) ta có: \(\widehat {BCM} = \widehat {CMD}\)
Mà góc BCM và CMD co le trong do đó: BC // DM.
Cách 2:
Gọi N là trung điểm của MD
Xét hai tam giác HAI và HMI có:
HA = HM (gt)
\(\widehat {AHI} = \widehat {MHI}( = {90^0})\)
IH là cạnh chung.
Do đó: \(\Delta HAI = \Delta HMI(c.g.c) \Rightarrow IA = IM,\widehat {HAI} = \widehat {HMI}.\)
Mà IA = ID \((\Delta ABI = \Delta DCI) \Rightarrow IM = ID\)
Xét tam giác IMN và IDN có:
IM = ID
IN là cạnh chung
MN = DN (N là trung điểm của MD)
Do đó: \(\Delta IMN = \Delta IDN(c.c.c) \)
\(\Rightarrow \widehat {IMN} = \widehat {IDN}.\)
Ta có:
\(\widehat {HAI} + \widehat {IDN} = \widehat {HMI} + \widehat {IMN} \)
\(\Rightarrow \widehat {MAD} + \widehat {ADM} = \widehat {AMD}\)
Tam giác AMD có: \(\widehat {MAD} + \widehat {ADM} + \widehat {AMD} = {180^0}.\)
Do đó: \(\widehat {AMD} + \widehat {AMD} = {180^0} \)
\(\Rightarrow 2\widehat {AMD} = {180^0} \Rightarrow \widehat {AMD} = {90^0} \Rightarrow AM \bot DM\)
Ta có: \(AM \bot BC;AM \bot DM.\) Vậy BC // DM.
Bài tập 13 trang 157 Toán 7 tập 1 là một phần quan trọng trong chương trình học Toán 7, tập trung vào việc củng cố kiến thức về các phép toán với số hữu tỉ. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản như số hữu tỉ, phép cộng, trừ, nhân, chia số hữu tỉ, và các quy tắc ưu tiên thực hiện phép tính.
Bài tập 13 thường bao gồm các dạng bài tập sau:
Để giải bài tập 13 trang 157 Toán 7 tập 1, học sinh có thể áp dụng các phương pháp sau:
Ví dụ 1: Tính giá trị của biểu thức sau:
(1/2) + (2/3) - (1/6)
Giải:
Để tính giá trị của biểu thức này, ta quy đồng mẫu số của các phân số:
(1/2) = (3/6)
(2/3) = (4/6)
Vậy biểu thức trở thành:
(3/6) + (4/6) - (1/6) = (3 + 4 - 1)/6 = 6/6 = 1
Để củng cố kiến thức và kỹ năng giải bài tập, học sinh có thể tự giải các bài tập sau:
Để học tốt môn Toán 7, học sinh cần:
Bài tập 13 trang 157 Toán 7 tập 1 là một bài tập quan trọng giúp học sinh củng cố kiến thức về các phép toán với số hữu tỉ. Bằng cách nắm vững các khái niệm cơ bản, áp dụng các phương pháp giải phù hợp, và luyện tập thường xuyên, học sinh có thể tự tin giải bài tập và đạt kết quả tốt trong môn Toán.