Bài tập 36 trang 125 thuộc chương trình Toán 7 tập 2, là một phần quan trọng trong quá trình ôn luyện và củng cố kiến thức của học sinh. Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững phương pháp giải và tự tin làm bài.
Chúng tôi không chỉ cung cấp đáp án mà còn phân tích từng bước giải, giúp học sinh hiểu rõ bản chất của bài toán.
Giải bài tập Cho tam giác ABC cân tại A. Trung tuyến BM và CN cắt nhau tại H.
Đề bài
Cho tam giác ABC cân tại A. Trung tuyến BM và CN cắt nhau tại H.
a) Chứng minh BM = CN
b) Chứng minh tam giác BHC cân.
c) Cho biết AH = 8 cm, BC = 18 cm. Tính AB.
Lời giải chi tiết
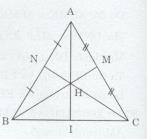
a) Ta có: \(AN{\rm{ }} = {\rm{ }}BN{\rm{ }} = {{AB} \over 2}\) (N là trung điểm của AB)
\(AM = MC = {{AB} \over 2}\) (M là trung điểm của AC)
AB = AC (∆ABC cân tại A)
Do đó AN = AM = BN = MC.
Xét ∆BMA và ∆CNA ta có: AB = AC (∆ABC cân tại A)
\(\widehat {BAM}\) chung
AM = AN
Do đó: ∆BMA = ∆CAN (c.g.c) => BM = CN.
b) Xét ∆BMC và ∆CNB ta có: BC (cạnh chung)
MC = BN
BM = CN (câu a)
Do đó: ∆BMC = ∆CNB (c.c.c) \( \Rightarrow \widehat {HBC} = \widehat {HCB}\). Vậy ∆BHC cân tại H.
c) Gọi I là giao điểm của AH và BC
∆ABC có hai đường trung tuyến BM và CN cắt nhau tại H (gt)
=> H là trọng tâm của ∆ABC
=> AI là đường trung tuyến của ∆ABC (vì AI đi qua H)
Ta có \(AH = {2 \over 3}AI \Rightarrow AI = {3 \over 2}AH = {3 \over 2}.8 = 12(cm)\)
Vì I là trung điểm của BC \( \Rightarrow BI = {{BC} \over 2} = {{18} \over 2} = 9(cm)\)
∆ABC cân tại A có AI là đường trung tuyến
Nên AI là đường cao \( \Rightarrow AI \bot BC\) tại I
Xét ∆ABI vuông tại I => AB2 = AI2 + BI2 (định lí Pythagore)
Nên AB2 = 122 + 92 = 225.
Do đó AB2 = 152. Vậy AB = 15 (cm).
Bài tập 36 trang 125 Toán 7 tập 2 thuộc chương trình đại số, thường liên quan đến các chủ đề như biểu thức đại số, đơn thức, đa thức, hoặc các bài toán về phương trình bậc nhất một ẩn. Để giải quyết bài tập này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản và áp dụng linh hoạt các quy tắc, định lý đã học.
Trước khi đi vào giải chi tiết, chúng ta cùng xem lại đề bài của Bài tập 36 trang 125 Toán 7 tập 2. (Ở đây cần có nội dung đề bài cụ thể, ví dụ: 'Tìm x biết: 2x + 5 = 11'). Yêu cầu của bài tập thường là tìm giá trị của biến, chứng minh một đẳng thức, hoặc giải một bài toán thực tế.
Để giải Bài tập 36 trang 125, chúng ta sẽ sử dụng phương pháp (ví dụ: chuyển vế, cộng trừ hai vế, nhân chia hai vế). Dưới đây là lời giải chi tiết:
Để giúp học sinh hiểu rõ hơn về phương pháp giải, chúng ta sẽ xem xét một ví dụ minh họa tương tự:
(Ví dụ minh họa với đề bài tương tự và lời giải chi tiết)
Dưới đây là một số bài tập tương tự để học sinh luyện tập:
Khi giải Bài tập 36 trang 125 Toán 7 tập 2, học sinh cần lưu ý những điều sau:
Kiến thức về biểu thức đại số và phương trình có ứng dụng rất lớn trong thực tế, ví dụ như trong việc tính toán chi phí, lợi nhuận, hoặc giải quyết các bài toán về vật lý, hóa học.
Bài tập 36 trang 125 Toán 7 tập 2 là một bài tập quan trọng giúp học sinh củng cố kiến thức về đại số. Hy vọng với lời giải chi tiết và các ví dụ minh họa, học sinh sẽ tự tin hơn khi giải các bài tập tương tự. Hãy luyện tập thường xuyên để nắm vững kiến thức và đạt kết quả tốt trong học tập.
| Chủ đề | Kiến thức liên quan |
|---|---|
| Biểu thức đại số | Đơn thức, đa thức, cộng trừ đa thức |
| Phương trình bậc nhất một ẩn | Chuyển vế, cộng trừ hai vế, nhân chia hai vế |