Chào mừng bạn đến với bài giải chi tiết Bài 7 trang 176 Tài liệu dạy – học Toán 7 tập 1 tại giaitoan.edu.vn. Chúng tôi cung cấp đáp án chính xác và phương pháp giải bài tập rõ ràng, giúp bạn nắm vững kiến thức Toán 7.
Bài viết này sẽ hướng dẫn bạn từng bước giải quyết các bài tập trong Bài 7, đồng thời cung cấp các kiến thức nền tảng cần thiết để bạn hiểu sâu hơn về chủ đề này.
Giải bài tập Cho tam giác ABC vuông tại A. GỌi M là trung điểm của BC, trên tia đối của tia MA lấy điểm D sao cho M là trung điểm của AD.
Đề bài
Cho tam giác ABC vuông tại A. GỌi M là trung điểm của BC, trên tia đối của tia MA lấy điểm D sao cho M là trung điểm của AD.
a) Chứng minh rằng \(\Delta MAB = \Delta MDC.\)
b) Chứng minh rằng \(CD \bot AC.\)
c) Gọi N là trung điểm của AC. Chứng minh rằng NB = ND.
d) Cho \(\widehat {ABC} = {60^0}.\) Chứng minh rằng \(\Delta MAB\) đều. Tinh AC khi biết AB = 8 cm.
Lời giải chi tiết
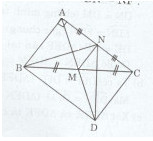
a)Xét tam giác MAB và MDC có:
MA = MD (M là trung điểm của AD)
MB = MC (M là trung điểm của BC)
\(\widehat {AMB} = \widehat {DMC}\) (hai góc đối đỉnh)
Do đó: \(\Delta MAB = \Delta MDC(c.g.c).\)
b) Ta có: \(\widehat {ABM} = \widehat {DCM}(\Delta MAB = \Delta MDC)\)
Mà góc ABM và DCM so le trong. Do đó: AB // CD.
Ta có: \(AB \bot AC(\Delta ABC\) vuông tại A) và AB // CD (chứng minh trên) \(\Rightarrow CD \bot AC.\)
c) Xét tam giác ANB và CND ta có:
AN = CN (N là trung điểm của AC)
\(\eqalign{ & \widehat {BAN} = \widehat {NCD}( = {90^0}) \cr & AB = CD(\Delta MAB = \Delta MDC) \cr} \)
Do đó: \(\Delta ANB = \Delta CND(c.g.c) \Rightarrow NB = ND\)
d) Xét tam giác ABC và CDA có:
AB = CD
\(\widehat {BAC} = \widehat {DCA}( = {90^0})\)
AC là cạnh chung.
Do đó: \(\Delta ABC = \Delta CDA(c.g.c) \Rightarrow BC = AD\)
Mà \(MB = MC = {{BC} \over 2}\) (M là trung điểm của BC)
Và \(MA = MD = {{AD} \over 2}\) (M là trung điểm của AD)
Do đó: MB = MC = MA = MD.
Tam giác MAB có MB = MA => tam giác MAB cân tại M
Mà \(\widehat {ABC} = {60^0}(gt)\) . Do đó tam giác MAB đều => MB = AB = 8cm.
Ta có: BC = 2MB = 2.8 = 16 (cm)
Tam giác ABC vuông tại A
\(\Rightarrow A{B^2} + A{C^2} = B{C^2}\) (định lí Pythagore)
Do đó: \(A{C^2} = B{C^2} - A{B^2} = {16^2} - {8^2} = 256 - 64 = 192\)
Mà AC > 0. Vậy \(AC = \sqrt {192} (cm).\)
Bài 7 trang 176 Toán 7 tập 1 thuộc chương trình học Toán 7, tập trung vào việc ôn tập và củng cố các kiến thức đã học trong chương. Bài tập trong bài này thường bao gồm các dạng bài tập về biểu thức đại số, phương trình bậc nhất một ẩn, và các bài toán thực tế liên quan đến các khái niệm này.
Bài 7 trang 176 thường bao gồm các bài tập sau:
Đề bài: Thu gọn biểu thức sau: 3x + 2y - x + 5y - 2x
Giải:
3x + 2y - x + 5y - 2x = (3x - x - 2x) + (2y + 5y) = 0x + 7y = 7y
Đề bài: Tính giá trị của biểu thức 2x - 3y khi x = 2 và y = -1
Giải:
2x - 3y = 2(2) - 3(-1) = 4 + 3 = 7
Đề bài: Giải phương trình: x + 5 = 10
Giải:
x + 5 = 10
x = 10 - 5
x = 5
Đề bài: Một người có 20000 đồng. Người đó mua 3 cái bút bi, mỗi cái giá 2000 đồng. Hỏi người đó còn lại bao nhiêu tiền?
Giải:
Số tiền mua 3 cái bút bi là: 3 * 2000 = 6000 đồng
Số tiền còn lại là: 20000 - 6000 = 14000 đồng
Trong quá trình giải các bài tập về biểu thức đại số, bạn cần nắm vững các quy tắc về thu gọn biểu thức, tìm giá trị của biểu thức, và các phép toán cộng, trừ, nhân, chia đa thức. Đối với các bài tập về phương trình bậc nhất một ẩn, bạn cần nắm vững các bước giải phương trình và các quy tắc biến đổi tương đương.
Ngoài sách giáo khoa, bạn có thể tham khảo thêm các tài liệu sau để học tốt môn Toán 7:
Hy vọng với bài giải chi tiết và hướng dẫn cụ thể này, bạn đã có thể tự tin giải các bài tập trong Bài 7 trang 176 Tài liệu dạy – học Toán 7 tập 1. Chúc bạn học tốt và đạt kết quả cao trong môn Toán!