Chào mừng các em học sinh đến với lời giải Bài tập 9 trang 94 Toán 7 tập 1. Bài tập này thuộc chương trình học Toán 7, tập trung vào việc rèn luyện kỹ năng giải toán về các phép toán với số hữu tỉ.
Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập tương tự.
Giải bài tập Cho y là hàm số của biến số x. Giá trị tương ứng của x, y được cho trong bảng sau:
Đề bài
Cho y là hàm số của biến số x. Giá trị tương ứng của x, y được cho trong bảng sau:
x | -2 | -1 | 0 | 1 | 2 |
y | -2 | -1 | 0 | 1 | 2 |
a) Vẽ một hệ trục tọa độ Oxy và xác định các điểm biểu diễn các cặp giá trị (x ; y) tương ứng có trong bảng trên.
b) Em có nhận xét gì về các điểm vừa xác định trong câu a ?
Lời giải chi tiết
a)
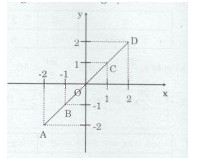
b) Năm điểm A, O, B, C, D thẳng hàng.
Bài tập 9 trang 94 Toán 7 tập 1 yêu cầu chúng ta thực hiện các phép tính với số hữu tỉ. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các quy tắc về cộng, trừ, nhân, chia số hữu tỉ, cũng như quy tắc chuyển đổi phân số về dạng tối giản.
Trước khi bắt đầu giải bài tập, hãy đọc kỹ đề bài để hiểu rõ yêu cầu. Xác định các số hữu tỉ cần thực hiện phép tính và loại phép tính cần sử dụng. Đảm bảo rằng bạn đã hiểu rõ các khái niệm liên quan đến số hữu tỉ.
Có một số phương pháp giải bài tập về số hữu tỉ mà bạn có thể áp dụng:
Để minh họa, chúng ta sẽ cùng giải một ví dụ cụ thể từ Bài tập 9 trang 94 Toán 7 tập 1. Giả sử đề bài yêu cầu tính:
(1/2) + (2/3) - (1/4)
Mẫu số chung nhỏ nhất của 2, 3 và 4 là 12. Do đó, chúng ta quy đồng các phân số như sau:
Thay các phân số đã quy đồng vào biểu thức ban đầu, ta có:
(6/12) + (8/12) - (3/12) = (6 + 8 - 3) / 12 = 11/12
Phân số 11/12 không thể rút gọn thêm nữa vì 11 và 12 không có ước chung nào khác 1.
Vậy, kết quả của phép tính (1/2) + (2/3) - (1/4) là 11/12.
Để củng cố kiến thức và kỹ năng giải bài tập về số hữu tỉ, bạn nên luyện tập thêm với các bài tập tương tự. Hãy tìm các bài tập trong sách giáo khoa, sách bài tập hoặc trên các trang web học toán online.
Số hữu tỉ được ứng dụng rộng rãi trong thực tế, ví dụ như:
Để học tốt môn Toán 7, bạn nên:
Hy vọng rằng lời giải chi tiết và phương pháp giải Bài tập 9 trang 94 Toán 7 tập 1 này sẽ giúp các em học sinh hiểu bài và tự tin giải các bài tập tương tự. Chúc các em học tốt!