Bài tập 9 trang 96 Toán 7 tập 1 là một bài tập quan trọng trong chương trình học Toán 7. Bài tập này yêu cầu học sinh vận dụng các kiến thức đã học về số nguyên, phép toán trên số nguyên để giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho Bài tập 9 trang 96 Toán 7 tập 1, giúp học sinh nắm vững kiến thức và tự tin làm bài tập.
Giải bài tập Vẽ một hệ trục tọa độ Oxy và đánh dấu các điểm M(0 ; 2), N(0 ; 1), P(0 ; 4).
Đề bài
Vẽ một hệ trục tọa độ Oxy và đánh dấu các điểm M(0 ; 2), N(0 ; 1), P(0 ; 4).
a) Em có nhận xét gì về các điểm M, N, P ?
b) Em hãy cho biết một điểm bất kì trên trục tung có hoành độ bằng bao nhiêu ?
Lời giải chi tiết
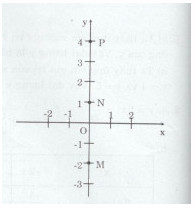
a)Ba điểm M, N, P cùng nằm trên trục tung.
b) Một điểm bất kì trên trục tung có hoành độ bằng 0.
Bài tập 9 trang 96 Toán 7 tập 1 thuộc chương trình đại số lớp 7, tập trung vào việc vận dụng các quy tắc về số nguyên, phép cộng, trừ, nhân, chia số nguyên để giải quyết các bài toán thực tế. Dưới đây là lời giải chi tiết và phương pháp giải bài tập này:
Cho các số nguyên a, b, c, d. Chứng minh rằng:
Để chứng minh các đẳng thức trên, ta sẽ sử dụng các quy tắc về dấu ngoặc và phép toán trên số nguyên.
Ta có:
Vậy, a - (b - c) = a - b + c.
Ta có:
Vậy, (a - b) - c = a - b - c.
Để giải các bài tập về quy tắc dấu ngoặc và phép toán trên số nguyên, cần nắm vững các quy tắc sau:
Áp dụng các quy tắc trên, ta có thể giải các bài tập tương tự như sau:
Ví dụ: Tính giá trị của biểu thức: 5 - (2 + 3)
Lời giải:
Để củng cố kiến thức, các em có thể tự giải thêm các bài tập sau:
Bài tập 9 trang 96 Toán 7 tập 1 là một bài tập cơ bản nhưng quan trọng trong chương trình học Toán 7. Việc nắm vững các quy tắc về dấu ngoặc và phép toán trên số nguyên sẽ giúp các em giải quyết các bài tập tương tự một cách dễ dàng và hiệu quả.