Bài tập 8 trang 156 thuộc chương trình Toán 7 tập 1, là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về các phép toán với số hữu tỉ. Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và tự tin giải bài tập.
Chúng tôi không chỉ cung cấp đáp án mà còn phân tích phương pháp giải, giúp học sinh hiểu rõ bản chất của bài toán và áp dụng vào các bài tập tương tự.
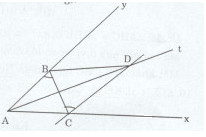
Giải bài tập Cho góc xAy nhọn có At là tia phân giác. Trên tia At ta lấy điểm D, đường thẳng song song với Ay kẻ từ D cắt Ax tại C.
Đề bài
Cho góc xAy nhọn có At là tia phân giác. Trên tia At ta lấy điểm D, đường thẳng song song với Ay kẻ từ D cắt Ax tại C.
a) Chứng minh rằng \(\widehat {CAD} = \widehat {CDA}\)
b) Trên Ay, lấy điểm B sao cho AB = AC. Chứng minh rằng \(\Delta ACD = \Delta ABD\)
c) Chứng minh rằng AC = DB và AC // DB.
Lời giải chi tiết
a)Ay // DC (gt)\( \Rightarrow \widehat {yAD} = \widehat {ADC}\) (hai góc so le trong).
Mà \(\widehat {yAD} = \widehat {CAD}\) (At là tia phân giác góc xAy)
Do đó: \(\widehat {CAD} = \widehat {ADC}\)
b) Xét tam giác ACD và ABD có:
AC = AB (gt)
\(\widehat {CAD} = \widehat {BAD}\) (At là tia phân giác của góc xAy)
AD là cạnh chung.
Do đó: \(\Delta ACD = \Delta ABD(c.g.c)\)
c) \(Ay//CD \Rightarrow \widehat {ABC} = \widehat {DCB}\) (hai góc so le trong)
\(\Delta ACD = \Delta ABD\) (chứng minh câu b) \( \Rightarrow \widehat {ACD} = \widehat {ABD}\)
Mà \(\widehat {DBC} + \widehat {ABC} = \widehat {ABD};\widehat {ACB} + \widehat {BCD} = \widehat {ACD}.\) Nên \(\widehat {DBC} = \widehat {ACB}\)
Xét tam giác ABC và DCB có:
\(\eqalign{ & \widehat {ABC} = \widehat {DCB}(cmt) \cr & \widehat {ACB} = \widehat {DBC}(cmt) \cr} \)
BC là cạnh chung.
Do đó: \(\Delta ABC = \Delta DCB(g.c.g) \Rightarrow AC = BD\)
Ta có: \(\widehat {DBC} = \widehat {BCA}\) (chứng minh trên)
Mà hai góc này ở vị trí so le trong nên BD // AC.
Bài tập 8 trang 156 Toán 7 tập 1 yêu cầu học sinh thực hiện các phép tính với số hữu tỉ. Để giải bài tập này, học sinh cần nắm vững các quy tắc về cộng, trừ, nhân, chia số hữu tỉ, cũng như quy tắc chuyển đổi phân số về dạng tối giản.
Trước khi bắt đầu giải bài tập, học sinh cần đọc kỹ đề bài để hiểu rõ yêu cầu. Xác định các số hữu tỉ cần thực hiện phép tính và loại phép tính cần sử dụng. Ví dụ, nếu đề bài yêu cầu tính tổng của hai phân số, học sinh cần tìm mẫu số chung và quy đồng mẫu số trước khi cộng.
Có một số phương pháp giải bài tập về số hữu tỉ mà học sinh có thể áp dụng:
Để minh họa, chúng ta sẽ cùng giải một số bài tập cụ thể trong Bài tập 8 trang 156 Toán 7 tập 1:
Vậy, (1/2) + (2/3) = (7/6).
Vậy, (3/4) - (1/5) = (11/20).
Nhân hai phân số: (2/5) * (3/7) = (2*3)/(5*7) = (6/35).
Vậy, (2/5) * (3/7) = (6/35).
Để nắm vững kiến thức về các phép toán với số hữu tỉ, học sinh nên luyện tập thêm nhiều bài tập khác. Giaitoan.edu.vn cung cấp một kho bài tập phong phú, đa dạng, giúp học sinh rèn luyện kỹ năng và tự tin giải bài tập.
Số hữu tỉ được ứng dụng rộng rãi trong thực tế, ví dụ như:
Để học tập môn Toán hiệu quả, học sinh nên:
Giaitoan.edu.vn hy vọng rằng với những hướng dẫn chi tiết và phương pháp giải bài tập hiệu quả, các em học sinh sẽ tự tin hơn trong việc học tập môn Toán.