Bài tập 7 trang 128 thuộc chương trình Toán 7 tập 2, tập trung vào việc rèn luyện kỹ năng giải toán về các phép toán với số hữu tỉ. Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Chúng tôi luôn cập nhật nhanh chóng và chính xác đáp án các bài tập trong sách giáo khoa Toán 7 tập 2, đảm bảo hỗ trợ tối đa cho quá trình học tập của bạn.
Giải bài tập Cho tam giác ABC vuông tại A. Tia phân giác của góc C cắt AB ở M
Đề bài
Cho tam giác ABC vuông tại A. Tia phân giác của góc C cắt AB ở M. Từ B kẻ BH vuông góc với đường thẳng CM \(\left( {H \in CM} \right)\). Trên tia đối của tia HC lấy điểm E sao cho HE = HM.
a) Chứng minh rằng tam giác MBE cân.
b) Chứng minh rằng \(\widehat {EBH} = \widehat {ACM}\)
c) Chứng minh rằng \(EB \bot BC\)
d) Đường thẳng BE cắt đường thẳng AC tại N. Tia phân giác \(\widehat {NAB}\) cắt đường thẳng BH tại D, tia ND cắt CM tại F. Tính số đo \(\widehat {NFC}\)
Lời giải chi tiết
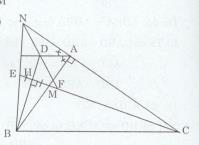
a) ∆MBE có: BH là đường cao (\(BH \bot EM\) tại H)
BH là đường trung tuyến (HE = HM, \(H \in EM\))
Nên ∆MBE cân tại B.
b) ∆MBE cân tại B có BH là đường cao
=> BH cũng là đường phân giác \( \Rightarrow \widehat {EBH} = \widehat {HBM}\)
Ta có: \(\widehat {HBM} + \widehat {BMH} = 90^\circ\) (∆HMB vuông tại H)
\(\widehat {ACM} + \widehat {AMC} = 90^\circ\) (∆AMC vuông tại A)
\(\widehat {BMH} = \widehat {AMC}\) (đối đỉnh)
Do đó \(\widehat {HBM} = \widehat {ACM}.\)
Mà \(\widehat {HBM} = \widehat {EBH}.\)
Nên \(\widehat {ACM} = \widehat {EBH}.\)
c) Ta có: \(\widehat {EBH} = {1 \over 2}\widehat {EBM}\) (BH là tia phân giác của \(\widehat {EBM}\))
\(\widehat {ACM} = {1 \over 2}\widehat {ACB}\) (CM là tia phân giác của \(\widehat {ACB}\))
\(\widehat {EBH} = \widehat {ACM}\) (câu b)
Do đó \(\widehat {EBM} = \widehat {ACB}.\)
Mà \(\widehat {ACB} + \widehat {MBC} = 90^\circ\) (∆ABC vuông tại A). Nên \(\widehat {EBM} + \widehat {MBC} = 90^\circ\).
\( \Rightarrow \widehat {EBC} = 90^\circ\). Vậy\(EB \bot BC.\)
d) ∆ABN có: AD là đường phân giác (gt)
BD là đường phân giác và AD cắt BD tại D (gt)
=> D là giao điểm ba đường phân giác của tam giác ABN
=> ND là đường phân giác của ∆ABN \( \Rightarrow \widehat {ANF} = {1 \over 2}\widehat {BNC}\)
Mà \(\widehat {NCF} = {1 \over 2}\widehat {NCB}\) (CF là tia phân giác của \(\widehat {NCB}\))
\(\widehat {BNC} + \widehat {NCB} = 90^\circ\) (∆NBC vuông tại B)
Nên \(\widehat {ANF} + \widehat {NCF} = {1 \over 2}\widehat {BNC} + {1 \over 2}\widehat {NCB} = {1 \over 2}(\widehat {BNC} + \widehat {NCB}) = {1 \over 2}.90^\circ = 45^\circ .\)
Lại có \(\widehat {NFC} + \widehat {ANF} + \widehat {NCF} = 180^\circ\) (tổng ba góc trong tam giác)
\( \Rightarrow \widehat {NFC} + 45^\circ = 180^\circ \Rightarrow \widehat {NFC} = 135^\circ\)
Bài tập 7 trang 128 Toán 7 tập 2 là một phần quan trọng trong chương trình học Toán 7, giúp học sinh củng cố kiến thức về các phép toán với số hữu tỉ, đặc biệt là phép nhân và chia số hữu tỉ. Để giải quyết bài tập này một cách hiệu quả, học sinh cần nắm vững các quy tắc và tính chất cơ bản của các phép toán này.
Bài tập 7 bao gồm các câu hỏi yêu cầu học sinh thực hiện các phép tính nhân và chia số hữu tỉ, đồng thời áp dụng các quy tắc về dấu của số hữu tỉ. Các bài tập thường được trình bày dưới dạng phân số hoặc số thập phân, đòi hỏi học sinh phải chuyển đổi linh hoạt giữa các dạng số này để thực hiện phép tính một cách chính xác.
Để giải bài tập 7 trang 128 Toán 7 tập 2, học sinh có thể áp dụng các bước sau:
Ví dụ 1: Tính (-2/3) * (3/4)
Giải:
Ví dụ 2: Tính (-5/7) : (2/3)
Giải:
Việc giải bài tập 7 trang 128 Toán 7 tập 2 không chỉ giúp học sinh củng cố kiến thức về các phép toán với số hữu tỉ mà còn rèn luyện kỹ năng giải toán, tư duy logic và khả năng áp dụng kiến thức vào thực tế. Đây là nền tảng quan trọng để học sinh tiếp thu các kiến thức toán học nâng cao hơn trong tương lai.
Giaitoan.edu.vn là một website học toán online uy tín, cung cấp đầy đủ các tài liệu học tập, bài giảng, bài tập và đáp án môn Toán 7. Chúng tôi cam kết mang đến cho học sinh những trải nghiệm học tập tốt nhất, giúp các em tự tin chinh phục môn Toán.
| Phép toán | Quy tắc |
|---|---|
| Nhân hai số hữu tỉ cùng dấu | Kết quả là một số hữu tỉ dương |
| Nhân hai số hữu tỉ khác dấu | Kết quả là một số hữu tỉ âm |
| Chia hai số hữu tỉ cùng dấu | Kết quả là một số hữu tỉ dương |
| Chia hai số hữu tỉ khác dấu | Kết quả là một số hữu tỉ âm |
Hy vọng với những hướng dẫn chi tiết và ví dụ minh họa trên, các em học sinh sẽ tự tin giải quyết bài tập 7 trang 128 Toán 7 tập 2 một cách hiệu quả. Chúc các em học tập tốt!