Chào mừng các em học sinh đến với lời giải Bài tập 12 trang 96 Toán 7 tập 2. Bài tập này thuộc chương trình học Toán 7, tập trung vào việc rèn luyện kỹ năng giải toán về các phép toán với số hữu tỉ.
Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập tương tự.
Giải bài tập Cho hình vẽ sau:
Đề bài
Cho hình vẽ sau:
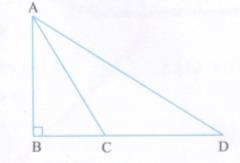
So sánh độ dài AB, AC, AD.
Lời giải chi tiết
Ta có BC, BD lần lượt là hình chiếu của đường xiên AC, AD trên đường thẳng BD và BC < BD (vì \(C \in BD\))
=> AC < AD (quan hệ giữa hình chiếu và đường xiên)
Mà AB < AC (đường vuông góc ngắn hơn đường xiên). Nên AB < AC < AD.
Bài tập 12 trang 96 Toán 7 tập 2 là một phần quan trọng trong chương trình học Toán 7, tập trung vào việc củng cố kiến thức về các phép toán với số hữu tỉ. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản như số hữu tỉ, phép cộng, trừ, nhân, chia số hữu tỉ, và các quy tắc ưu tiên thực hiện phép tính.
Bài tập 12 trang 96 Toán 7 tập 2 thường bao gồm các dạng bài tập sau:
Để giải bài tập 12 trang 96 Toán 7 tập 2, học sinh có thể áp dụng các bước sau:
Ví dụ 1: Tính giá trị của biểu thức sau:
(1/2) + (2/3) - (3/4)
Giải:
Để tính giá trị của biểu thức này, ta cần tìm mẫu số chung của các phân số. Mẫu số chung nhỏ nhất của 2, 3, và 4 là 12. Do đó, ta có:
(1/2) + (2/3) - (3/4) = (6/12) + (8/12) - (9/12) = (6 + 8 - 9)/12 = 5/12
Ví dụ 2: Tìm x trong phương trình sau:
x + (1/3) = (2/5)
Giải:
Để tìm x, ta cần chuyển (1/3) sang vế phải của phương trình:
x = (2/5) - (1/3)
Tương tự như ví dụ 1, ta tìm mẫu số chung của 5 và 3 là 15. Do đó, ta có:
x = (6/15) - (5/15) = 1/15
Khi giải bài tập 12 trang 96 Toán 7 tập 2, học sinh cần lưu ý những điều sau:
Để hỗ trợ học sinh trong quá trình giải bài tập 12 trang 96 Toán 7 tập 2, các em có thể tham khảo các tài liệu sau:
Bài tập 12 trang 96 Toán 7 tập 2 là một bài tập quan trọng giúp học sinh củng cố kiến thức về các phép toán với số hữu tỉ. Bằng cách nắm vững các khái niệm cơ bản, áp dụng các bước giải đúng, và luyện tập thường xuyên, học sinh có thể tự tin giải bài tập này và đạt kết quả tốt trong môn Toán.