Bài tập Hoạt động 9 trang 166 Toán 7 tập 1 là một phần quan trọng trong chương trình học Toán lớp 7. giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Chúng tôi không chỉ cung cấp đáp án mà còn giải thích rõ ràng từng bước, giúp học sinh hiểu bản chất của bài toán và áp dụng vào các bài tập tương tự.
Giải bài tập Bài toán : Cho tam giác ABC và tam giác EDI
Đề bài
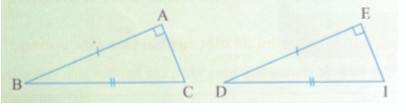
Bài toán : Cho tam giác ABC và tam giác EDI có \(\widehat A = \widehat E = {90^0},BC = DI,AB = ED.\)
Chứng minh rằng \(\Delta ABC = \Delta EDI.\)
Hãy điền vào chỗ trống (….) để hoàn chỉnh phần chứng minh bài toán đã cho :
GT | \(\eqalign{ & \Delta ABC,\widehat A = {90^0} \cr & \Delta EDI,\widehat E = {90^0} \cr & AB = ED,BC = DI \cr} \) |
KL | \(\Delta ABC = \Delta EDI\) |
Chứng minh :
Xét \(\Delta ABC\) vuông tại A, theo định lí Pytagore ta có :
\(B{C^2} = ... + ...\)
Nên \(A{C^2} = ... + ...(1)\)
Xét tam giác EDI vuông tại E, theo định lí Pytagore ta có :
\(... = D{E^2} + E{I^2}\)
Nên \(E{I^2} = ... - ...(2)\)
Mà AB = ED, BC = DI (…) (3)
Từ (1), (2), (3) suy ra \(A{C^2} = E{I^2}\) nên AC = …
Từ đó suy ra \(\Delta ABC = \Delta EDI(...)\)
Lời giải chi tiết
Chứng minh :
Xét \(\Delta ABC\) vuông tại A, theo định lí Pytagore ta có :
\(B{C^2} = A{B^2} + A{C^2}\)
Nên \(A{C^2} = B{C^2} - A{B^2}(1)\)
Xét tam giác EDI vuông tại E, theo định lí Pytagore ta có :
\(D{I^2} = D{E^2} + E{I^2}\)
Nên \(E{I^2} = D{I^2} - D{E^2}(2)\)
Mà AB = ED, BC = DI (gt) (3)
Từ (1), (2), (3) suy ra \(A{C^2} = E{I^2}\) nên AC = EI
Từ đó suy ra \(\Delta ABC = \Delta EDI(c.c.c)\)
Hoạt động 9 trang 166 Toán 7 tập 1 thuộc chương trình học Toán 7, tập trung vào việc vận dụng các kiến thức đã học về số hữu tỉ, phép cộng, trừ, nhân, chia số hữu tỉ để giải quyết các bài toán thực tế. Bài tập này thường yêu cầu học sinh phải phân tích đề bài, xác định đúng các yếu tố cần tìm và lựa chọn phương pháp giải phù hợp.
Hoạt động 9 thường bao gồm các dạng bài tập sau:
Để giải quyết hiệu quả các bài tập trong Hoạt động 9 trang 166 Toán 7 tập 1, học sinh cần nắm vững các kiến thức sau:
Dưới đây là một ví dụ minh họa cách giải một bài tập trong Hoạt động 9:
Bài tập: Tính (-2/3) + (1/2)
Giải:
Vậy, kết quả của phép tính là -1/6.
Để học tập hiệu quả môn Toán 7, đặc biệt là các bài tập về số hữu tỉ, học sinh nên:
Số hữu tỉ có ứng dụng rất rộng rãi trong thực tế, ví dụ như:
Hoạt động 9 trang 166 Toán 7 tập 1 là một bài tập quan trọng giúp học sinh củng cố kiến thức về số hữu tỉ và rèn luyện kỹ năng giải toán. Bằng cách nắm vững lý thuyết, luyện tập thường xuyên và tìm kiếm sự giúp đỡ khi cần thiết, học sinh có thể giải quyết hiệu quả các bài tập trong hoạt động này và đạt kết quả tốt trong môn Toán 7.
| Dạng bài tập | Phương pháp giải |
|---|---|
| Tính toán số hữu tỉ | Quy đồng mẫu số, thực hiện các phép tính cộng, trừ, nhân, chia. |
| Tìm số hữu tỉ | Lập phương trình, giải phương trình để tìm số hữu tỉ cần tìm. |
| Ứng dụng số hữu tỉ | Phân tích đề bài, xác định các yếu tố liên quan đến số hữu tỉ, vận dụng kiến thức để giải quyết bài toán. |