Bài tập 34 trang 124 thuộc chương trình Toán 7 tập 2, là một phần quan trọng trong quá trình ôn luyện và củng cố kiến thức của học sinh. Bài tập này thường tập trung vào các chủ đề như biểu thức đại số, phương trình bậc nhất một ẩn, hoặc các ứng dụng thực tế của toán học.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho Bài tập 34 trang 124, giúp học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Giải bài tập Cho tam giác DEF cân tại D, kẻ trung tuyến EM. Trên tia đối của tia ME lấy điểm N sao cho MN = ME.
Đề bài
Cho tam giác DEF cân tại D, kẻ trung tuyến EM. Trên tia đối của tia ME lấy điểm N sao cho
MN = ME.
a) Chứng minh DE = FN và tam giác DFN cân.
b) Trên tia đối của FD, lấy điểm A sao cho FA = FD. Chứng minh F là trọng tâm của tam giác NEA.
c) Chứng minh tam giác DNA vuông
d) Kẻ đường cao EB của tam giác AEN. Chứng minh ba điểm E, F, B thẳng hàng.
Lời giải chi tiết
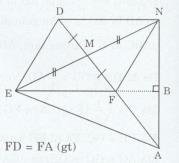
a) Xét ∆DEM và ∆FNM
Ta có: DM = MF (M là trung điểm của DF)
\(\widehat {DME} = \widehat {NMF}\) (đối đỉnh)
EM = MN (gt)
Do đó: ∆DEM = ∆FNM (c.g.c) => DE = FN
Mà DE = DF (∆DEF cân tại D). Nên FN=DF
Do đó ∆DNF cân tại F.
b) Ta có \(MF = {1 \over 2}FD\) (M là trung điểm của DF) và FD = FA (gt)
\( \Rightarrow MF = {1 \over 2}FA \Rightarrow {{MF} \over {FA}} = {1 \over 2} \Rightarrow {{AM - FA} \over {FA}} = {1 \over 2} \Rightarrow {{AM} \over {FA}} - 1 = {1 \over 2} \Rightarrow {{AM} \over {FA}} = {3 \over 2} \Rightarrow AF = {2 \over 3}AM\)
∆EAN có AM là đường trung tuyến (EM = MN, \(M \in EN\))
F thuộc đoạn thẳng AM và \(AF = {2 \over 3}AM\)
Do đó F là trọng tâm của tam giác NEA.
c) Ta có FN = FA (= DF) => ∆FAN cân tại F \( \Rightarrow \widehat {FNA} = \widehat {FAN}\)
Mà \(\widehat {FND} = \widehat {FDN}\) (∆DNF cân tại F). Do đó \(\widehat {DNA} = \widehat {FND} + \widehat {FNA} = \widehat {FAN} + \widehat {FDN}\)
∆DNA có \(\widehat {DNA} + \widehat {FAN} + \widehat {FDN} = 180^\circ\)
Do đó \(\widehat {DNA} + \widehat {DNA} = 180^\circ \Rightarrow 2\widehat {DNA} = 180^\circ \Rightarrow \widehat {DNA} = 90^\circ\)
Vậy tam giác DNA vuông tại N.
d) Xét ∆DMN và ∆EMF ta có: DM = MF
\(\widehat {NMD} = \widehat {EMF}\) (đối đỉnh)
MN = EM (gt)
Do đó: ∆DMN = ∆FME (c.g.c) \( \Rightarrow \widehat {DNM} = \widehat {MEF}\)
Mà \(\widehat {DNM}\) và \(\widehat {MEF}\) ở vị trí so le trong. Nên DN // EF
Mặt khác \(DN \bot NA\) (∆DNA vuông tại N). Do đó \(EF \bot NA\)
Ta có: \(EF \bot NA\) và \(EB \bot NA\) (EB là đường cao của ∆AEN)
Do đó EF trùng với EB. Vậy E, F, B thẳng hàng.
Bài tập 34 trang 124 Toán 7 tập 2 là một bài tập quan trọng trong chương trình học, giúp học sinh rèn luyện kỹ năng giải toán và áp dụng kiến thức đã học vào thực tế. Để giúp các em học sinh giải bài tập này một cách hiệu quả, giaitoan.edu.vn xin giới thiệu lời giải chi tiết và hướng dẫn giải bài tập 34 trang 124 Toán 7 tập 2.
Bài tập 34 trang 124 Toán 7 tập 2 thường bao gồm các dạng bài tập khác nhau, như:
Để giải bài tập 34 trang 124 Toán 7 tập 2, các em cần nắm vững các kiến thức cơ bản về biểu thức đại số, phương trình bậc nhất một ẩn và các ứng dụng thực tế của toán học. Dưới đây là lời giải chi tiết cho một số bài tập thường gặp:
Lời giải:
Thay x = 2 và y = -1 vào biểu thức 3x + 2y, ta được:
3x + 2y = 3(2) + 2(-1) = 6 - 2 = 4
Vậy giá trị của biểu thức 3x + 2y khi x = 2 và y = -1 là 4.
Lời giải:
Chuyển -5 sang vế phải, ta được:
2x = 3 + 5
2x = 8
Chia cả hai vế cho 2, ta được:
x = 4
Vậy nghiệm của phương trình 2x - 5 = 3 là x = 4.
Để giải bài tập 34 trang 124 Toán 7 tập 2 một cách hiệu quả, các em cần:
Để rèn luyện kỹ năng giải toán và củng cố kiến thức, các em có thể luyện tập thêm các bài tập tương tự trong sách giáo khoa và các tài liệu tham khảo khác. Ngoài ra, các em cũng có thể tham gia các khóa học toán online tại giaitoan.edu.vn để được hướng dẫn và giải đáp thắc mắc bởi các giáo viên giàu kinh nghiệm.
Bài tập 34 trang 124 Toán 7 tập 2 là một bài tập quan trọng trong chương trình học. Hy vọng với lời giải chi tiết và hướng dẫn giải bài tập mà giaitoan.edu.vn cung cấp, các em học sinh sẽ giải bài tập này một cách hiệu quả và đạt kết quả tốt nhất.