Bài tập Hoạt động 2 trang 59 Toán 7 tập 2 là một phần quan trọng trong chương trình học Toán 7. Bài tập này giúp học sinh rèn luyện kỹ năng áp dụng kiến thức đã học vào giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho bài tập này, giúp các em học sinh nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Giải bài tập Điền vào ô trống thích hợp :
Đề bài
Điền vào ô trống thích hợp :
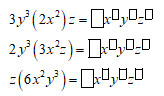
Cả ba đơn thức \(3{y^3}\left( {2{x^2}} \right)z\) , \(2{y^3}\left( {3{x^2}z} \right)\) và \(z\left( {6{x^2}{y^3}} \right)\) đều bằng \(6{x^2}{y^3}z.\) Ta nói \(6{x^2}{y^3}z\) là đơn thức thu gọn của ba đơn thức này với 6 là hệ số, \({x^2}{y^3}z\) là phần biến.
Lời giải chi tiết
\(\eqalign{ & 3{y^3}\left( {2{x^2}} \right)z = 6{x^2}{y^3}{z^1} \cr & 2{y^3}\left( {3{x^2}z} \right) = 6{x^2}{y^3}{z^1} \cr & z\left( {6{x^2}{y^3}} \right) = 6{x^2}{y^3}{z^1} \cr} \)
Hoạt động 2 trang 59 Toán 7 tập 2 thuộc chương trình đại số, thường liên quan đến các bài toán về biểu thức đại số, đơn thức, đa thức hoặc các phép toán trên chúng. Để giải quyết bài tập này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản về:
Trước khi bắt đầu giải bài tập, học sinh cần đọc kỹ đề bài, xác định rõ yêu cầu của bài toán. Sau đó, phân tích các dữ kiện đã cho và tìm ra mối liên hệ giữa chúng. Việc vẽ sơ đồ hoặc sử dụng các ký hiệu toán học có thể giúp học sinh hình dung rõ hơn về bài toán.
Tùy thuộc vào từng dạng bài tập cụ thể, các bước giải có thể khác nhau. Tuy nhiên, một số bước giải chung mà học sinh có thể áp dụng bao gồm:
Giả sử bài tập Hoạt động 2 trang 59 yêu cầu tính giá trị của biểu thức: 3x2 + 2x - 5 khi x = 2.
Giải:
Thay x = 2 vào biểu thức, ta được:
3(2)2 + 2(2) - 5 = 3(4) + 4 - 5 = 12 + 4 - 5 = 11
Vậy, giá trị của biểu thức 3x2 + 2x - 5 khi x = 2 là 11.
Để giải bài tập Hoạt động 2 trang 59 một cách chính xác và hiệu quả, học sinh cần lưu ý một số điều sau:
Ngoài sách giáo khoa, học sinh có thể tham khảo thêm các tài liệu sau để hỗ trợ học tập:
Kiến thức về đơn thức, đa thức và biểu thức đại số có ứng dụng rộng rãi trong nhiều lĩnh vực của đời sống và khoa học kỹ thuật. Ví dụ, trong vật lý, các công thức tính vận tốc, gia tốc, lực thường được biểu diễn dưới dạng các biểu thức đại số. Trong kinh tế, các mô hình dự báo doanh thu, lợi nhuận cũng sử dụng các biểu thức đại số. Do đó, việc nắm vững kiến thức này là rất quan trọng.
Hoạt động 2 trang 59 Toán 7 tập 2 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải toán đại số. Bằng cách nắm vững các kiến thức cơ bản, phân tích bài toán một cách cẩn thận và thực hiện các bước giải một cách chính xác, học sinh có thể tự tin giải quyết bài tập này và đạt kết quả tốt trong môn Toán.