Chào mừng bạn đến với bài giải chi tiết Bài 3 trang 168 Toán 7 tập 1 tại giaitoan.edu.vn. Chúng tôi cung cấp đáp án chính xác và lời giải dễ hiểu, giúp bạn nắm vững kiến thức và tự tin giải các bài tập tương tự.
Bài 3 thuộc chương trình học Toán 7 tập 1, tập trung vào việc rèn luyện kỹ năng giải toán và áp dụng các kiến thức đã học vào thực tế.
Giải bài tập Cho tam giác ABC cân tại A, biết
Đề bài
Cho tam giác ABC cân tại A, biết \(\widehat A = {50^0}\) (h.17).
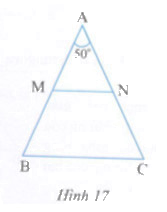
a) Tính \(\widehat B,\widehat C.\)
b) Gọi M, N lần lượt là trung điểm của AB, AC. Chứng minh rằng cân.
c) Chứng minh rằng MN // BC.
Lời giải chi tiết
a)Tam giác ABC có: \(\widehat A + \widehat B + \widehat C = {180^0}.\) Mà \(\widehat B = \widehat C(\Delta ABC\) cân tại A) nên \({50^0} + \widehat B + \widehat B = {180^0}\)
\(\Rightarrow {50^0} + 2\widehat B = {180^0} \Rightarrow 2\widehat B = {180^0} - {50^0} = {130^0} \Rightarrow \widehat B = {{{{130}^0}} \over 2} = {65^0}.\)
Ta có: \(\widehat C = \widehat B = {65^0}\)
b) Ta có: \(AM = {{AB} \over 2}\) (M là trung điểm của AB)
\(AN = {{AC} \over 2}\) (N là trung điểm của AC)
AB = AC (tam giác ABC cân tại A)
Suy ra Am = AN. Do đó: tam giác AMN cân tại A.
c) Tam giác AMN có: \(\widehat A + \widehat {AMN} + \widehat {ANM} = {180^0}\) mà \(\widehat {AMN} = \widehat {ANM}(\Delta AMN\) cân tại A)
Nên \(\widehat A + 2\widehat {AMN} = {180^0} \Rightarrow \widehat {AMN} = {{{{180}^0} - {{50}^0}} \over 2} = {65^0}.\)
Mà \(\widehat B = {65^0}\) (chứng minh câu a) nên \(\widehat {AMN} = \widehat B( = {65^0}).\)
Góc AMN và B là hai góc đồng vị. Do đó MN // BC.
Bài 3 trang 168 Toán 7 tập 1 là một bài tập quan trọng trong chương trình học, giúp học sinh củng cố kiến thức về các phép toán cơ bản và cách áp dụng chúng vào giải quyết các bài toán thực tế. Bài tập này thường yêu cầu học sinh thực hiện các phép tính cộng, trừ, nhân, chia với các số hữu tỉ, đồng thời rèn luyện kỹ năng biến đổi biểu thức và tìm giá trị của biểu thức.
Bài 3 thường bao gồm một số câu hỏi nhỏ, yêu cầu học sinh:
Để giải bài 3 trang 168 Toán 7 tập 1 một cách hiệu quả, học sinh cần:
Giả sử bài 3 có một câu hỏi như sau:
Tính: (1/2) + (2/3) - (1/6)
Lời giải:
(1/2) + (2/3) - (1/6) = (3/6) + (4/6) - (1/6) = (3 + 4 - 1)/6 = 6/6 = 1
Ngoài các phép tính cơ bản, bài 3 trang 168 còn có thể xuất hiện các dạng bài tập sau:
Khi giải bài 3 trang 168 Toán 7 tập 1, học sinh cần lưu ý:
Để học tốt Toán 7 tập 1, học sinh có thể tham khảo các tài liệu sau:
Bài 3 trang 168 Toán 7 tập 1 là một bài tập quan trọng, giúp học sinh củng cố kiến thức và rèn luyện kỹ năng giải toán. Hy vọng với hướng dẫn chi tiết và các ví dụ minh họa trên, các em học sinh sẽ tự tin giải bài tập và đạt kết quả tốt trong môn Toán.