Bài tập 7 trang 156 thuộc chương trình Toán 7 tập 1, tập trung vào việc rèn luyện kỹ năng giải toán về các phép toán với số hữu tỉ. Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và phương pháp giải.
Chúng tôi hiểu rằng việc tự học đôi khi gặp khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn bài giải này với mục tiêu hỗ trợ tối đa cho học sinh trong quá trình học tập.
Giải bài tập Cho tam giác ABC nhọn (AB < AC), phân giác của góc A cắt BC tại D. Trên AC lấy điểm E sao cho AE = AB.
Đề bài
Cho tam giác ABC nhọn (AB < AC), phân giác của góc A cắt BC tại D. Trên AC lấy điểm E sao cho AE = AB.
a) Chứng minh rằng \(\Delta ADB = \Delta ADE\)
b) Đường thẳng ED cắt đường thẳng AB tại F. Chứng minh rằng AF = AC.
c) Chứng minh rằng \(\Delta DBF = \Delta DEC\)
Lời giải chi tiết
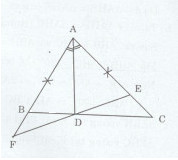
a)Xét tam giác ADB và ADE có:
AB = AE (gt)
\(\widehat {BAD} = \widehat {EAD}\) (AD là tia phân giác của góc BAC)
AD là cạnh chung.
Do đó: \(\Delta ADB = \Delta ADE(c.g.c)\)
b) Ta có: \(\Delta ADB = \Delta ADE\) (chứng minh câu a)
Suy ra: \(\widehat {ABD} = \widehat {AED}\) và BD = ED
Xét tam giác AEF và ABC có:
\(\widehat {EAF} = \widehat {BAC}\) (góc chung)
AE = AB (gt)
\(\widehat {AEF} = \widehat {ABC}(\widehat {ABD} = \widehat {AED})\)
Do đó: \(\Delta AEF = \Delta ABC(g.c.g) \Rightarrow AF = AC\)
c) Ta có: \(\eqalign{ & \widehat {ABD} + \widehat {DBF} = {180^0} \cr & \widehat {AED} + \widehat {DEC} = {180^0} \cr} \) (hai góc kề bù)
Mà \(\widehat {ABD} = \widehat {AED}\) (chứng minh câu b) nên \(\widehat {DBF} = \widehat {DEC}\)
Xét tam giác BFD và ECD có:
\(\widehat {FBD} = \widehat {CED}(cmt)\)
BD = ED (chứng minh câu b)
\(\widehat {BDF} = \widehat {EDC}\) (hai góc đối đỉnh)
Do đó: \(\Delta BFD = \Delta ECD(g.c.g)\)
Bài tập 7 trang 156 Toán 7 tập 1 là một phần quan trọng trong chương trình học, giúp học sinh củng cố kiến thức về các phép toán với số hữu tỉ. Dưới đây là giải chi tiết từng bài tập, kèm theo phương pháp giải để học sinh hiểu rõ hơn:
a) (1/2) + (1/3)
Để cộng hai phân số, ta cần quy đồng mẫu số. Mẫu số chung nhỏ nhất của 2 và 3 là 6. Do đó:
(1/2) + (1/3) = (3/6) + (2/6) = (3+2)/6 = 5/6
b) (2/5) - (1/4)
Tương tự, ta quy đồng mẫu số của 5 và 4 là 20:
(2/5) - (1/4) = (8/20) - (5/20) = (8-5)/20 = 3/20
c) (3/4) * (2/7)
Khi nhân hai phân số, ta nhân tử số với tử số và mẫu số với mẫu số:
(3/4) * (2/7) = (3*2)/(4*7) = 6/28 = 3/14
d) (5/6) : (1/2)
Khi chia hai phân số, ta nhân phân số thứ nhất với nghịch đảo của phân số thứ hai:
(5/6) : (1/2) = (5/6) * (2/1) = (5*2)/(6*1) = 10/6 = 5/3
a) (1/2) + (1/3) * (2/5)
Theo thứ tự thực hiện các phép tính, ta thực hiện phép nhân trước, sau đó thực hiện phép cộng:
(1/2) + (1/3) * (2/5) = (1/2) + (2/15) = (15/30) + (4/30) = 19/30
b) (3/4) - (1/2) : (1/3)
Tương tự, ta thực hiện phép chia trước, sau đó thực hiện phép trừ:
(3/4) - (1/2) : (1/3) = (3/4) - (3/2) = (3/4) - (6/4) = -3/4
a) x + (1/2) = (3/4)
Để tìm x, ta trừ cả hai vế của phương trình cho (1/2):
x = (3/4) - (1/2) = (3/4) - (2/4) = 1/4
b) x - (2/5) = (1/3)
Để tìm x, ta cộng cả hai vế của phương trình cho (2/5):
x = (1/3) + (2/5) = (5/15) + (6/15) = 11/15
Để nắm vững kiến thức và kỹ năng giải bài tập về số hữu tỉ, các em nên luyện tập thêm các bài tập tương tự trong sách giáo khoa và các tài liệu tham khảo khác. Giaitoan.edu.vn sẽ tiếp tục cung cấp các bài giải chi tiết và phương pháp giải cho các bài tập khác trong chương trình Toán 7 tập 1.
Bài tập 7 trang 156 Toán 7 tập 1 là một bài tập quan trọng giúp học sinh củng cố kiến thức về các phép toán với số hữu tỉ. Hy vọng với lời giải chi tiết và phương pháp giải được trình bày trên đây, các em sẽ tự tin hơn trong việc giải các bài tập tương tự.