Chào mừng các em học sinh đến với lời giải chi tiết Bài tập 30 trang 124 Tài liệu dạy – học Toán 7 tập 2. Bài tập này thuộc chương trình học Toán 7, tập trung vào việc rèn luyện kỹ năng giải toán và áp dụng kiến thức đã học.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải dễ hiểu, phương pháp giải khoa học và các bài tập tương tự để giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Giải bài tập Cho tam giác ABC vuông tại A (AB < AC)
Đề bài
Cho tam giác ABC vuông tại A (AB < AC). Tia phân giác của góc B cắt AC tại M. Kẻ MN vuông góc với BC \(\left( {N \in BC} \right)\)
a) Chứng minh rằng tam giác ABM bằng tam giác NBM.
b) Chứng minh AN vuông góc với BM.
c) Kẻ đường cao AH của tam giác ABC. Chứng minh AN là tia phân giác của góc HAM.
d) Gọi I là giao điểm của AH với BM. Chứng minh rằng NI vuông góc với ABN.
Lời giải chi tiết
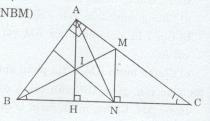
a) Xét ∆ABM \((\widehat A = 90^\circ )\) và ∆NBM \((\widehat N = 90^\circ )\)
Ta có: BM (cạnh chung)
\(\widehat {ABM} = \widehat {NBM}\) (BM là tia phân giác của \(\widehat {ABC}\))
Do đó: ∆ABM = ∆NBM (cạnh huyền – góc nhọn).
b) Ta có BA = BN và MA = MN (∆ABM = ∆NBM)
=> BM là đường trung trực của AN
\( \Rightarrow BM \bot AN.\)
c) Ta có AM = NM (∆ABM = ∆NBM)
=> ∆AMN cân tại M
\( \Rightarrow \widehat {MNA} = \widehat {NAM}\)
Mà \(\widehat {MNA} = \widehat {NAH}\) (hai góc so le trong và AH // MN (vì cùng vuông góc với BC))
Nên \(\widehat {NAM} = \widehat {NAH} \Rightarrow\) AH là tia phân giác của \(\widehat {HAM}.\)
d) BA = BN (∆ABM = ∆NBM) => ∆ABN cân tại B.
Mà BI là đường phân giác của ∆ABN (gt). Nên BI cũng là đường cao của ∆ABN.
Lại có AH là đường cao của ∆ABN (\(AH \bot BN\) tại H) và BI cắt AH tại I (gt)
=> I là trực tâm của ∆ABN => NI là đường cao của ∆ABN \( \Rightarrow NI \bot AB.\)
Bài tập 30 trang 124 Toán 7 tập 2 là một bài tập quan trọng trong chương trình học Toán 7, tập trung vào việc vận dụng các kiến thức về biểu thức đại số, các phép toán với số hữu tỉ và các tính chất của chúng. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản và các quy tắc tính toán.
Trước khi đi vào giải chi tiết, chúng ta cùng xem lại đề bài của Bài tập 30 trang 124 Toán 7 tập 2:
(Đề bài cụ thể sẽ được chèn vào đây - ví dụ: Tính giá trị của biểu thức: a) 3x + 5y khi x = 2, y = -1; b) 2(a - b) + 3(a + b) khi a = 1, b = -2)
Để giải bài tập này, chúng ta sẽ thực hiện theo các bước sau:
Ví dụ: (Giải thích chi tiết với đề bài ví dụ ở trên)
a) 3x + 5y khi x = 2, y = -1
Thay x = 2 và y = -1 vào biểu thức, ta được:
3 * 2 + 5 * (-1) = 6 - 5 = 1
Vậy, giá trị của biểu thức 3x + 5y khi x = 2, y = -1 là 1.
b) 2(a - b) + 3(a + b) khi a = 1, b = -2
Thay a = 1 và b = -2 vào biểu thức, ta được:
2(1 - (-2)) + 3(1 + (-2)) = 2(1 + 2) + 3(1 - 2) = 2 * 3 + 3 * (-1) = 6 - 3 = 3
Vậy, giá trị của biểu thức 2(a - b) + 3(a + b) khi a = 1, b = -2 là 3.
Để củng cố kiến thức và kỹ năng giải bài tập, các em có thể luyện tập thêm với các bài tập tương tự sau:
Khi giải Bài tập 30 trang 124 Toán 7 tập 2, các em cần lưu ý những điều sau:
Bài tập 30 trang 124 Toán 7 tập 2 là một bài tập quan trọng giúp các em rèn luyện kỹ năng giải toán và áp dụng kiến thức đã học. Hy vọng với lời giải chi tiết và các lưu ý trên, các em sẽ tự tin hơn trong quá trình học tập và đạt kết quả tốt nhất.