Chào mừng các em học sinh đến với lời giải Bài tập 3 trang 115 Toán 7 tập 1. Bài tập này thuộc chương trình học Toán 7, tập trung vào việc rèn luyện kỹ năng giải toán về các phép toán với số hữu tỉ.
Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập tương tự.
Giải bài tập Cho hai đường thẳng cắt nhau, trong bốn góc tạo thành có một góc có số đo bằng 50o.
Đề bài
Cho hai đường thẳng cắt nhau, trong bốn góc tạo thành có một góc có số đo bằng 50o.
a) Hãy kể tên các cặp góc đối đỉnh.
b) Tính số đo của ba góc còn lại.
Lời giải chi tiết
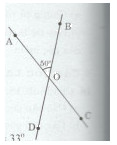
a)\(\widehat {AOB}\) và \(\widehat {DOC}\) là hai góc đối đỉnh.
\(\widehat {AOD}\) và \(\widehat {BOC}\) là hai góc đối đỉnh.
b) Giả sử \(\widehat {AOB} = {50^0}\)
Cần tính số đo các góc AOD, DOC, BOC.
Hai góc AOB và AOD là hai góc kề bù.
\( \Rightarrow \widehat {AOB} + \widehat {AOD} = {180^0}\)
Do đó: \(\widehat {AOD} = {180^0} - {50^0} = {130^0}\)
Ta có: \(\widehat {DOC} = \widehat {AOB}\) (hai góc đối đỉnh) nên \(\widehat {DOC} = {50^0}\)
Mặt khác \(\widehat {BOC} = \widehat {AOD}\) (hai góc đối đỉnh) nên \(\widehat {BOC} = {130^0}\)
Bài tập 3 trang 115 Toán 7 tập 1 là một phần quan trọng trong chương trình học Toán 7, tập trung vào việc củng cố kiến thức về các phép toán với số hữu tỉ. Để giúp các em học sinh hiểu rõ hơn và tự tin giải bài tập, giaitoan.edu.vn xin giới thiệu lời giải chi tiết và hướng dẫn giải bài tập này.
Bài tập 3 yêu cầu học sinh thực hiện các phép tính với số hữu tỉ, bao gồm phép cộng, trừ, nhân, chia. Các bài tập thường được trình bày dưới dạng các biểu thức số hoặc các bài toán thực tế liên quan đến số hữu tỉ.
Để giải bài tập 3 trang 115 Toán 7 tập 1, các em cần nắm vững các quy tắc sau:
Dưới đây là lời giải chi tiết cho từng phần của bài tập 3 trang 115 Toán 7 tập 1:
Ví dụ: Tính \frac{1}{2} + \frac{3}{4}\
Lời giải: Để cộng hai phân số có mẫu khác nhau, ta cần quy đồng mẫu số. Mẫu số chung nhỏ nhất của 2 và 4 là 4. Ta quy đồng phân số \frac{1}{2}\ thành \frac{2}{4}\. Vậy, \frac{1}{2} + \frac{3}{4} = \frac{2}{4} + \frac{3}{4} = \frac{5}{4}\
Ví dụ: Tính \frac{2}{3} - \frac{1}{6}\
Lời giải: Tương tự như phần a, ta quy đồng mẫu số. Mẫu số chung nhỏ nhất của 3 và 6 là 6. Ta quy đồng phân số \frac{2}{3}\ thành \frac{4}{6}\. Vậy, \frac{2}{3} - \frac{1}{6} = \frac{4}{6} - \frac{1}{6} = \frac{3}{6} = \frac{1}{2}\
Ví dụ: Tính \frac{1}{5} \times \frac{2}{7}\
Lời giải: Để nhân hai phân số, ta nhân tử số với tử số và mẫu số với mẫu số. Vậy, \frac{1}{5} \times \frac{2}{7} = \frac{1 \times 2}{5 \times 7} = \frac{2}{35}\
Ví dụ: Tính \frac{3}{4} : \frac{1}{2}\
Lời giải: Để chia hai phân số, ta nhân phân số thứ nhất với nghịch đảo của phân số thứ hai. Nghịch đảo của \frac{1}{2}\ là \frac{2}{1}\. Vậy, \frac{3}{4} : \frac{1}{2} = \frac{3}{4} \times \frac{2}{1} = \frac{3 \times 2}{4 \times 1} = \frac{6}{4} = \frac{3}{2}\
Để củng cố kiến thức và kỹ năng giải bài tập về số hữu tỉ, các em có thể luyện tập thêm các bài tập tương tự trong sách giáo khoa và các tài liệu tham khảo khác.
Bài tập 3 trang 115 Toán 7 tập 1 là một bài tập quan trọng giúp các em học sinh rèn luyện kỹ năng giải toán về số hữu tỉ. Hy vọng với lời giải chi tiết và hướng dẫn giải trên, các em sẽ tự tin giải bài tập và đạt kết quả tốt trong môn Toán.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục kiến thức Toán học.