Chào mừng bạn đến với bài giải chi tiết Bài 6 trang 175 Toán 7 tập 1 tại giaitoan.edu.vn. Chúng tôi cung cấp đáp án chính xác và phương pháp giải bài tập một cách dễ hiểu, giúp bạn nắm vững kiến thức và tự tin hơn trong học tập.
Bài viết này sẽ hướng dẫn bạn từng bước giải quyết các bài tập trong Bài 6 trang 175 Tài liệu dạy – học Toán 7 tập 1, đồng thời cung cấp các kiến thức nền tảng cần thiết để bạn hiểu rõ bản chất của vấn đề.
Giải bài tập Cho tam giác DEF cân tại D. Gọi I là trung điểm của EF.
Đề bài
Cho tam giác DEF cân tại D. Gọi I là trung điểm của EF.
a) Chứng minh rằng \(\Delta DIE = \Delta DIF.\)
b) Kẻ \(IM \bot DE(M \in DE),IN \bot DF(N \in DF).\) Chứng minh rằng \(\Delta IMN\) cân.
c) Chứng minh rằng MN // EF.
d) Chứng minh rằng
\(2I{N^2} = D{F^2} - D{N^2} - N{F^2}.\)
Lời giải chi tiết
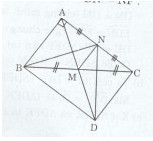
a)Xét tam giác DIE và DIF ta có:
DI là cạnh chung
IE = IF (I là trung điểm của EF)
DE = DF (tam giác DEF cân tại D)
Do đó: \(\Delta DIE = \Delta DIF(c.g.c).\)
b) Xét tam giác MDI vuông tại M và tam giác NDI vuông tại N có:
DI là cạnh chung.
\(\widehat {MDI} = \widehat {NDI}(\Delta DIE = \Delta DIF)\)
Do đó: (cạnh huyền - góc nhọn) => IM = IN.
Vậy tam giác IMN cân tại I.
c) Ta có: \(DM = DN(\Delta MDI = \Delta NDI) \Rightarrow \Delta DMN\) cân tại D \(\Rightarrow \widehat {DMN} = \widehat {DNM}\)
Mà \(\widehat {DMN} + \widehat {DNM} + \widehat {MDN} = {180^0}\) (tổng ba góc trong một tam giác)
Do đó: \(\widehat {DMN} = {{{{180}^0} - \widehat {MDN}} \over 2}(1)\)
Ta có: \(\widehat {DEF} = \widehat {DFE}(\Delta DEF\) cân tại D)
Mà \(\widehat {DEF} + \widehat {DFE} + \widehat {EDF} = {180^0}\) (tổng ba góc trong một tam giác)
Do đó: \(\widehat {DEF} = {{{{180}^0} - \widehat {EDF}} \over 2} = {{{{180}^0} - \widehat {MDN}} \over 2}(2)\)
Tà (1) và (2) suy ra: \(\widehat {DMN} = \widehat {DEF}\)
Mà hai góc DMN và DEF đồng vị. Do đó: MN // EF.
d) Ta có: \(\widehat {DIE} = \widehat {DIF}(\Delta DIE = \Delta DIF)\)
Mà \(\widehat {DIE} + \widehat {DIF} = {180^0}\) (kề bù). Do đó: \(\widehat {DIF} + \widehat {DIF} = {180^0} \Rightarrow 2\widehat {DIF} = {180^0} \Rightarrow \widehat {DIF} = {90^0}\)
Tam giác IDF vuông tại I\(\Rightarrow I{D^2} + I{F^2} = D{F^2}\) (định lí Pythagore)
Tam giác NDI vuông tại N \(\Rightarrow I{N^2} + D{N^2} = I{D^2} \Rightarrow I{N^2} = I{D^2} - D{N^2}\) (định lí Pythagore)
Tam giác NIF vuông tại N \(I{N^2} + N{F^2} = I{F^2} \Rightarrow I{N^2} = I{F^2} - N{F^2}\) (định lí Pythagore)
Do đó: \(2N{I^2} = I{D^2} - D{N^2} + I{F^2} - N{F^2} = (I{D^2} + I{F^2}) - D{N^2} - N{F^2} = D{F^2} - D{N^2} - N{F^2}\)
Bài 6 trang 175 Toán 7 tập 1 thuộc chương trình học Toán 7, tập trung vào việc vận dụng các kiến thức đã học về biểu thức đại số để giải các bài toán thực tế. Bài tập này thường yêu cầu học sinh phải hiểu rõ các quy tắc về dấu ngoặc, thứ tự thực hiện các phép tính, và các tính chất của phép cộng, trừ, nhân, chia.
Bài 6 thường bao gồm các dạng bài tập sau:
Để giải Bài 6 trang 175 Toán 7 tập 1 một cách hiệu quả, bạn cần:
Ví dụ 1: Tính giá trị của biểu thức 3x + 2y khi x = 2 và y = -1.
Giải:
Thay x = 2 và y = -1 vào biểu thức, ta được:
3x + 2y = 3(2) + 2(-1) = 6 - 2 = 4
Vậy, giá trị của biểu thức 3x + 2y khi x = 2 và y = -1 là 4.
Ví dụ 2: Rút gọn biểu thức 2(x + 3) - 5x.
Giải:
2(x + 3) - 5x = 2x + 6 - 5x = (2x - 5x) + 6 = -3x + 6
Vậy, biểu thức 2(x + 3) - 5x được rút gọn thành -3x + 6.
Để củng cố kiến thức và kỹ năng giải Bài 6 trang 175 Toán 7 tập 1, bạn có thể luyện tập thêm với các bài tập tương tự trong sách giáo khoa và các tài liệu tham khảo khác. Ngoài ra, bạn cũng có thể tìm kiếm các bài giải chi tiết trên internet hoặc tham gia các khóa học toán online để được hướng dẫn và giải đáp thắc mắc.
Việc nắm vững kiến thức và kỹ năng giải Bài 6 trang 175 Toán 7 tập 1 là rất quan trọng vì nó là nền tảng cho việc học các kiến thức nâng cao hơn trong chương trình Toán 7 và các chương trình học tiếp theo. Ngoài ra, nó cũng giúp bạn phát triển tư duy logic, khả năng giải quyết vấn đề, và kỹ năng tính toán.
Hy vọng rằng bài viết này đã cung cấp cho bạn những thông tin hữu ích và giúp bạn giải Bài 6 trang 175 Toán 7 tập 1 một cách dễ dàng và hiệu quả. Chúc bạn học tập tốt!