Chào mừng các em học sinh đến với lời giải Bài tập 4 trang 130 Toán 7 tập 2 - Hình học. Bài tập này thuộc chương trình học Toán 7, tập trung vào kiến thức về hình học cơ bản.
Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và rèn luyện kỹ năng giải toán hiệu quả.
Giải bài tập Tam giác ABC vuông tại A (AB < AC)
Đề bài
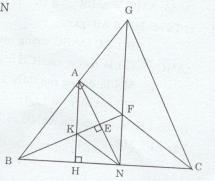
Tam giác ABC vuông tại A (AB < AC). Trên cạnh BC lấy điểm N sao cho BA = BN. Kẻ \(BE \bot AN\,\,\left( {E \in AN} \right)\)
a) Chứng minh BE là tia phân giác của góc ABN.
b) Kẻ đường cao AH của tam giác ABC. Gọi K là giao điểm của AH với BE. Chứng minh NK // CA.
c) Đường thẳng BK cắt AC tại F. Gọi G là giao điểm của đường thẳng AB với NF. Chứng minh tam giác GBC cân.
Lời giải chi tiết
a) BA = BN => ∆ABN cân tại B.
Mà BE là đường cao của ∆ABN (vì \(BE \bot AN\) tại E)
Nên BE cũng là đường phân giác của ∆ABN
Vậy BE là tia phân giác của \(\widehat {ABN}.\)
b) ∆ABN có hai đường cao BE và AH cắt nhau tại K (gt).
=> K là trực tâm của ∆ABN
=> NK là đường cao của ∆ABN
\( \Rightarrow NK \bot AB\)
Mà \(CA \bot AB\) (∆ABC vuông tại A)
Nên NK // CA.
c) Ta có: \(\widehat {NFC} = \widehat {FNK}\) (hai góc so le trong và NK // AC)
\(\widehat {NFC} = \widehat {AFG}\) (đối đỉnh)
\( \Rightarrow \widehat {FNK} = \widehat {AFG}\)
Mà \(\widehat {FNK}\) và \(\widehat {AFG}\) ở vị trí đồng vị. Nên AH // GN
Lại có \(AH \bot BC\) (AH là đường cao của ∆ABC) \( \Rightarrow GN \bot BC.\)
Xét ∆ABC và ∆GNB ta có \(\widehat {BAC} = \widehat {BNG}( = 90^\circ )\)
AB = BN (gt)
\(\widehat {ABC}\) chung
Do đó: ∆ABC = ∆NBG (g.c.g) => BC = BG
Vậy ∆BGC cân tại B.
Bài tập 4 trang 130 Toán 7 tập 2 thuộc chương trình Hình học, yêu cầu học sinh vận dụng các kiến thức đã học về góc, tia, đường thẳng để giải quyết các bài toán thực tế. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này:
Trước khi đi vào giải bài tập, chúng ta cần ôn lại một số kiến thức lý thuyết quan trọng:
(Giả sử đề bài Bài tập 4 là: Cho hình vẽ, biết góc AOB = 60° và góc BOC = 40°. Tính góc AOC.)
Lời giải:
Có hai trường hợp xảy ra:
Khi đó, góc AOC + góc BOC = góc AOB
=> góc AOC = góc AOB - góc BOC = 60° - 40° = 20°
Khi đó, góc AOB + góc BOC = góc AOC
=> góc AOC = góc AOB + góc BOC = 60° + 40° = 100°
Để củng cố kiến thức, các em có thể tự giải các bài tập tương tự sau:
Kiến thức về góc và các loại góc có ứng dụng rất lớn trong thực tế, đặc biệt trong các lĩnh vực như kiến trúc, xây dựng, hàng hải,... Việc nắm vững kiến thức này sẽ giúp các em giải quyết các bài toán thực tế một cách dễ dàng và hiệu quả.
Để giải tốt các bài tập Hình học, các em cần:
Giaitoan.edu.vn hy vọng với lời giải chi tiết và hướng dẫn giải bài tập 4 trang 130 Toán 7 tập 2 - Hình học này, các em sẽ học tập tốt hơn và đạt kết quả cao trong môn Toán.
| Bài tập | Lời giải |
|---|---|
| Bài tập 4 trang 130 | Xem chi tiết ở trên |