Chào mừng các em học sinh đến với lời giải Bài tập 8 trang 118 Toán 7 tập 1. Bài tập này thuộc chương trình học Toán 7, tập trung vào việc rèn luyện kỹ năng giải toán về các phép toán với số hữu tỉ.
Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và phương pháp giải bài tập hiệu quả.
Giải bài tập Cho hình 20, biết
Đề bài
Cho hình 20, biết \(\widehat {{A_2}} = {140^o},\,\,\widehat {{B_1}} = {40^o}\) . Tính số đo các góc còn lại.
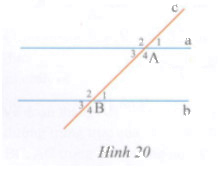
Lời giải chi tiết
Ta có: \(\widehat {{A_1}} + \widehat {{A_2}} = {180^0}\) (kề bù) nên \(\widehat {{A_1}} + {140^0} = {180^0}\)
\( \Rightarrow \widehat {{A_1}} = {180^0} - {140^0} = {40^0}\)
Mặt khác \(\widehat {{B_1}} + \widehat {{B_2}} = {180^0}\) (kề bù) nên \({40^0} + \widehat {{B_2}} = {180^0} \Rightarrow \widehat {{B_2}} = 180 - 40 = {140^0}\)
\(\widehat {{A_4}} = \widehat {{A_2}} = {140^0}\) (hai góc đối đỉnh)
\(\widehat {{B_3}} = \widehat {{B_1}} = {40^0}\) (hai góc đối đỉnh)
\(\widehat {{A_3}} = \widehat {{A_1}} = {40^0}\) (hai góc đối đỉnh)
\(\widehat {{B_4}} = \widehat {{B_2}} = {140^0}\) (hai góc đối đỉnh)
Bài tập 8 trang 118 Toán 7 tập 1 là một bài tập quan trọng trong chương trình học Toán 7, tập trung vào việc vận dụng các kiến thức về số hữu tỉ và các phép toán trên số hữu tỉ. Để giải bài tập này một cách hiệu quả, các em cần nắm vững các khái niệm cơ bản và các quy tắc tính toán.
Bài tập 8 yêu cầu các em thực hiện các phép tính với số hữu tỉ, bao gồm phép cộng, trừ, nhân, chia. Các số hữu tỉ có thể được biểu diễn dưới dạng phân số hoặc số thập phân. Để giải bài tập này, các em cần thực hiện các bước sau:
Ví dụ 1: Tính \frac{1}{2} + \frac{3}{4}
Giải:
Vậy, \frac{1}{2} + \frac{3}{4} = \frac{5}{4}
Ví dụ 2: Tính \frac{2}{3} \times \frac{5}{6}
Giải:
Vậy, \frac{2}{3} \times \frac{5}{6} = \frac{5}{9}
Ngoài sách giáo khoa, các em có thể tham khảo thêm các tài liệu sau để hỗ trợ giải bài tập:
Bài tập 8 trang 118 Toán 7 tập 1 là một bài tập quan trọng giúp các em củng cố kiến thức về số hữu tỉ và các phép toán trên số hữu tỉ. Hy vọng với hướng dẫn chi tiết và các ví dụ minh họa trên, các em sẽ giải bài tập này một cách hiệu quả và đạt kết quả tốt nhất.