Hoạt động 13 trang 20 Tài liệu dạy – học Toán 7 tập 1

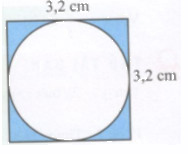
Hoạt động 13 trang 20 Toán 7 tập 1: Giải chi tiết và hướng dẫn

Hoạt động 13 trang 20 Toán 7 tập 1 thuộc chương trình đại số, tập trung vào việc vận dụng các kiến thức về số hữu tỉ, phép cộng, trừ, nhân, chia số hữu tỉ để giải quyết các bài toán thực tế. Bài tập này thường yêu cầu học sinh thực hiện các phép tính, so sánh số hữu tỉ, và tìm hiểu về tính chất của các phép toán.

Nội dung chính của Hoạt động 13 trang 20

Hoạt động 13 thường bao gồm các bài tập sau:

• Bài 1: Tính các biểu thức chứa số hữu tỉ.
• Bài 2: So sánh các số hữu tỉ.
• Bài 3: Tìm số hữu tỉ thỏa mãn các điều kiện cho trước.
• Bài 4: Ứng dụng các kiến thức về số hữu tỉ vào giải quyết các bài toán thực tế.

Hướng dẫn giải chi tiết

Để giải quyết các bài tập trong Hoạt động 13 trang 20, học sinh cần nắm vững các kiến thức sau:

1. Khái niệm về số hữu tỉ: Số hữu tỉ là số có thể được biểu diễn dưới dạng phân số a/b, trong đó a là số nguyên và b là số nguyên khác 0.
2. Phép cộng, trừ, nhân, chia số hữu tỉ: Nắm vững quy tắc thực hiện các phép toán này.
3. Tính chất của các phép toán: Giao hoán, kết hợp, phân phối.
4. So sánh số hữu tỉ: Sử dụng các phương pháp như quy đồng mẫu số, so sánh với 0, hoặc sử dụng tính chất bắc cầu.

Ví dụ minh họa

Ví dụ 1: Tính biểu thức (1/2) + (2/3).

Giải: Để tính biểu thức này, ta cần quy đồng mẫu số của hai phân số. Mẫu số chung nhỏ nhất của 2 và 3 là 6. Ta có:

(1/2) + (2/3) = (3/6) + (4/6) = (3+4)/6 = 7/6

Ví dụ 2: So sánh hai số hữu tỉ -1/2 và -2/3.

Giải: Ta quy đồng mẫu số của hai phân số. Mẫu số chung nhỏ nhất của 2 và 3 là 6. Ta có:

-1/2 = -3/6 và -2/3 = -4/6. Vì -3 > -4 nên -3/6 > -4/6, do đó -1/2 > -2/3.

Mẹo giải nhanh

Để giải nhanh các bài tập về số hữu tỉ, học sinh có thể áp dụng các mẹo sau:

• Sử dụng máy tính bỏ túi để thực hiện các phép tính phức tạp.
• Biến đổi các biểu thức về dạng đơn giản nhất trước khi tính toán.
• Luyện tập thường xuyên để nắm vững các quy tắc và tính chất.

Ứng dụng thực tế

Kiến thức về số hữu tỉ có ứng dụng rộng rãi trong đời sống thực tế, ví dụ như:

• Tính toán tiền bạc, đo lường.
• Giải quyết các bài toán về tỷ lệ, phần trăm.
• Phân tích dữ liệu thống kê.

Bài tập luyện tập thêm

Để củng cố kiến thức, học sinh có thể tự giải thêm các bài tập sau:

• Tính: (3/4) - (1/2)
• So sánh: 5/6 và 7/8
• Tìm x: x + (1/3) = (2/5)

Kết luận

Hoạt động 13 trang 20 Toán 7 tập 1 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải toán và củng cố kiến thức về số hữu tỉ. Bằng cách nắm vững các kiến thức cơ bản, áp dụng các mẹo giải nhanh, và luyện tập thường xuyên, học sinh có thể tự tin giải quyết các bài tập này một cách hiệu quả.