Chào mừng các em học sinh đến với lời giải chi tiết Bài tập 38 trang 99 Toán 7 tập 2. Bài tập này thuộc chương trình học Toán 7, tập trung vào việc rèn luyện kỹ năng giải toán về các phép toán với số hữu tỉ.
Giaitoan.edu.vn cung cấp lời giải dễ hiểu, phương pháp giải khoa học, giúp các em nắm vững kiến thức và tự tin giải các bài tập tương tự.
Giải bài tập Cho tam giác ABC có M thuộc tia phân giác ngoài của góc C. Trên tia đối của tia CA lấy điểm I sao cho CI = CB.
Đề bài
Cho tam giác ABC có M thuộc tia phân giác ngoài của góc C. Trên tia đối của tia CA lấy điểm I sao cho CI = CB.
a) So sánh MI với MB.
b) Chứng minh: MA + MB > AC + BC
Lời giải chi tiết
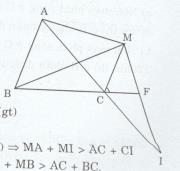
a) Gọi F là giao điểm của BC và MI
Ta có \(\widehat {MCB} = \widehat {MCA} + \widehat {ACB}\) và \(\widehat {MCI} = \widehat {MCF} + \widehat {FCI}\)
Mà \(\widehat {MCA} = \widehat {MCF}\)(CM là tia phân giác của \(\widehat {ACF}\))
Và \(\widehat {ACB} = \widehat {FCI}\) (đối đỉnh). Do đó \(\widehat {MCB} = \widehat {MCI}\)
Xét ∆MCB và ∆MCI ta có MC (cạnh chung)
\(\widehat {MCB} = \widehat {MCI}\) và BC = CI (gt)
Do đó ∆MCB = ∆MCI (c.g.c) => MB = MI.
b) ∆AMI có MA + MI > AI (bất đằng thức trong tam giác) => MA + MI > AC + CI
Mà BC = CI, MB = MI (∆MCB = ∆MCI). Do đó MA + MB > AC + BC.
Bài tập 38 trang 99 Toán 7 tập 2 là một bài tập quan trọng trong chương trình học Toán 7, tập trung vào việc vận dụng các kiến thức về số hữu tỉ, các phép toán cộng, trừ, nhân, chia số hữu tỉ để giải quyết các bài toán thực tế.
(Đề bài cụ thể của Bài tập 38 trang 99 sẽ được trình bày tại đây. Ví dụ: Tính: a) (1/2) + (1/3); b) (2/5) - (1/4); c) (3/7) * (2/5); d) (4/9) : (1/3))
Để giải bài tập này, chúng ta cần nắm vững các quy tắc sau:
Giải:
Để giải các bài tập về số hữu tỉ, các em cần:
Ví dụ 1: Tính (5/6) + (1/4).
Lời giải: MSC của 6 và 4 là 12. Ta có: (5/6) + (1/4) = (5*2)/(6*2) + (1*3)/(4*3) = 10/12 + 3/12 = 13/12
Ví dụ 2: Tính (3/8) - (1/6).
Lời giải: MSC của 8 và 6 là 24. Ta có: (3/8) - (1/6) = (3*3)/(8*3) - (1*4)/(6*4) = 9/24 - 4/24 = 5/24
Để rèn luyện thêm kỹ năng giải toán về số hữu tỉ, các em có thể tự giải các bài tập sau:
Bài tập 38 trang 99 Toán 7 tập 2 là một bài tập cơ bản nhưng quan trọng trong chương trình học Toán 7. Việc nắm vững các quy tắc và phương pháp giải sẽ giúp các em tự tin giải quyết các bài toán tương tự và đạt kết quả tốt trong môn học.
Hy vọng với lời giải chi tiết và phương pháp giải được trình bày trên đây, các em học sinh sẽ hiểu rõ hơn về Bài tập 38 trang 99 Toán 7 tập 2 và có thể tự tin giải các bài tập tương tự.