Chào mừng các em học sinh đến với lời giải Bài tập 3 trang 120 Toán 7 tập 2. Bài tập này thuộc chương trình học Toán 7, tập trung vào việc rèn luyện kỹ năng giải toán về các phép toán với số hữu tỉ.
Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và phương pháp giải bài tập hiệu quả.
Giải bài tập Cho tam giác nhọn ABC. Trung tuyến AM và CN cắt nhau tại G. Trên tia đối của tia MA lấy điểm E sao cho ME = MG.
Đề bài
Cho tam giác nhọn ABC. Trung tuyến AM và CN cắt nhau tại G. Trên tia đối của tia MA lấy điểm E sao cho ME = MG.
a) Chứng minh BG song song với EC.
b) Gọi I là trung điểm của BE, AI cắt BG tại F. Chứng minh : AF = 2FI.
Lời giải chi tiết
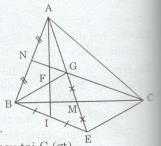
a) Xét ∆BMG và ∆CME ta có
BM = MC (M là trung điểm của BC)
\(\widehat {BMG} = \widehat {CME}\) (hai góc đối đỉnh)
Và GM = ME (gt)
Do đó: ∆BMG = ∆CME (c.g.c) \( \Rightarrow \widehat {BGM} = \widehat {CEM}\)
Mà \(\widehat {BGM}\) và \(\widehat {CEM}\) ở vị trí so le trong nên BG // EC.
b) ∆ABC có hai đường trung tuyến AM và CN cắt nhau tại G (gt)
=> G là trọng tâm của ∆ABC \( \Rightarrow AG = {2 \over 3}AM\)
Mà AG + GM = AM. Do đó \(GM = {1 \over 3}AM.\) Nên AG = 2GM.
Mà MG = ME => AG = GE. Vậy G là trung điểm của AE.
∆ABE có: BG và AI cắt nhau tại F (gt)
AI là đường trung tuyến (I là trung điểm của BE)
Và BG là đường trung tuyến (G là trung điểm của AE)
Do đó F là trọng tâm của tam giác ABE \( \Rightarrow AF = {2 \over 3}AI\)
Mà AF + FI = AI; \(FI = AI - {2 \over 3}AI = {1 \over 3}AI.\) Nên AF = 2FI.
Bài tập 3 trang 120 Toán 7 tập 2 là một phần quan trọng trong chương trình học Toán 7, tập trung vào việc củng cố kiến thức về các phép toán với số hữu tỉ. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản và các quy tắc tính toán.
Bài tập 3 thường bao gồm các dạng bài tập sau:
Để giải bài tập 3 trang 120 Toán 7 tập 2, học sinh có thể áp dụng các phương pháp sau:
Ví dụ 1: Tính \frac{1}{2} + \frac{3}{4}
Giải:
Để cộng hai phân số, ta cần quy đồng mẫu số:
\frac{1}{2} = \frac{2}{4}
Vậy, \frac{1}{2} + \frac{3}{4} = \frac{2}{4} + \frac{3}{4} = \frac{5}{4}
Ví dụ 2: Tính \frac{2}{3} \times \frac{1}{5}
Giải:
Để nhân hai phân số, ta nhân tử số với tử số và mẫu số với mẫu số:
\frac{2}{3} \times \frac{1}{5} = \frac{2 \times 1}{3 \times 5} = \frac{2}{15}
Để củng cố kiến thức và kỹ năng giải bài tập, học sinh nên luyện tập thêm các bài tập tương tự trong sách giáo khoa và các tài liệu tham khảo khác.
Số hữu tỉ được ứng dụng rộng rãi trong thực tế, ví dụ như:
Bài tập 3 trang 120 Toán 7 tập 2 là một bài tập quan trọng giúp học sinh củng cố kiến thức về các phép toán với số hữu tỉ. Bằng cách nắm vững các khái niệm cơ bản, áp dụng các phương pháp giải phù hợp và luyện tập thường xuyên, học sinh có thể giải bài tập này một cách hiệu quả và đạt kết quả tốt.