Bài tập 37 trang 125 Toán 7 tập 2 thuộc chương trình đại số lớp 7, tập trung vào việc vận dụng các kiến thức về biểu thức đại số, thu gọn biểu thức và tính giá trị của biểu thức. Bài tập này giúp học sinh rèn luyện kỹ năng giải toán và hiểu sâu hơn về các khái niệm đã học.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho Bài tập 37 trang 125 Toán 7 tập 2, giúp các em học sinh tự tin hơn trong quá trình học tập.
Giải bài tập Cho tam giác ABC vuông cân tại A có AM là trung tuyến. Lấy điểm D bất kì thuộc cạnh BC. Gọi H và K theo thứ tự là hình chiếu vuông góc cuả B và C xuống đường thẳng AD.
Đề bài
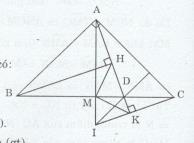
Cho tam giác ABC vuông cân tại A có AM là trung tuyến. Lấy điểm D bất kì thuộc cạnh BC. Gọi H và K theo thứ tự là hình chiếu vuông góc cuả B và C xuống đường thẳng AD.
a) Chứng minh tam giác AKC bằng tam giác BHA.
b) Gọi I là giao điểm của Am với CK. Chứng minh đường thẳng DI vuông góc với AC.
c) Chứng minh KM là tia phân giác góc HKI.
Lời giải chi tiết
a) Ta có: \(\widehat {BAH} + \widehat {DAC} = 90^\circ (\widehat {BAC} = 90^\circ )\)
\(\widehat {ACK} + \widehat {DAC} = 90^\circ\) (∆AKC vuông tại K)
Do đó \(\widehat {BAH} = \widehat {ACK}\)
Xét ∆AKC (\(\widehat {AKC} = 90^\circ\)) và ∆BHA (\)\widehat {BHA} = 90^\circ\)) có:
AC = AB (∆ABC vuông cân ở A)
Và \(\widehat {ACK} = \widehat {BAH}\)
Do đó: ∆AKC = ∆BHA (cạnh huyền – góc nhọn).
b) ∆ABC cân tại A có AM là đường trung tuyến (gt).
=> AM là đường cao của tam giác ABC. Vậy \(AM \bot BC\) tại M.
∆AIC có: AK là đường cao (\(AK \bot CI\) tại K)
CM là đường cao (\(CM \bot AI\) tại M)
AK cắt CM tại D (gt)
Do đó D là trực tâm của ∆AIC => ID là đường cao của ∆AIC. Vậy \(DI \bot AC.\)
c) ∆AMC vuông tại M (\(AM \bot BC\) tại M) có \(\widehat {ACM} = 45^\circ\) (∆ABC vuông cân tại A)
=> ∆AMC vuông cân tại M => AM = CM
Xét ∆AMH và ∆CMK có AM = CM
\(\widehat {MAH} = \widehat {MCK}\) (cùng phụ với góc AIK)
AH = CK (∆AKC = ∆BHA)
Do đó ∆AMH = ∆CMK (c.g.c) => MH = MK, \(\widehat {AMH} = \widehat {CMK}\)
Ta có \(\widehat {HMK} = \widehat {HMC} + \widehat {CMK} = \widehat {HMC} + \widehat {AMH} = \widehat {AMC} = 90^\circ\)
∆MHK vuông tại M có MH = MK.
=> ∆MHK vuông cân tại M \( \Rightarrow \widehat {MHK} = 45^\circ\). Mà\(\widehat {MKH} + \widehat {MKI} = \widehat {AKI} = 90^\circ\)
Nên \(\widehat {MKI} = 90^\circ - \widehat {MKH} = 90^\circ - 45^\circ = 45^\circ\)
Ta có \(\widehat {MKI} = \widehat {MKH}( = 45^\circ )\).Vậy KM là tia phân giác góc HKI.
Bài tập 37 trang 125 Toán 7 tập 2 là một phần quan trọng trong chương trình học Toán 7, tập trung vào việc củng cố kiến thức về biểu thức đại số. Để giải quyết bài tập này một cách hiệu quả, học sinh cần nắm vững các quy tắc về thu gọn biểu thức, cộng trừ đa thức và tính giá trị của biểu thức tại một giá trị cụ thể của biến.
Bài tập 37 thường bao gồm các dạng bài tập sau:
Để giải bài tập 37 trang 125 Toán 7 tập 2 một cách hiệu quả, học sinh có thể tham khảo các bước sau:
Ví dụ 1: Thu gọn biểu thức sau: 3x + 2y - x + 5y
Giải:
3x + 2y - x + 5y = (3x - x) + (2y + 5y) = 2x + 7y
Ví dụ 2: Tính giá trị của biểu thức 2x - 3y khi x = 1 và y = -2
Giải:
2x - 3y = 2(1) - 3(-2) = 2 + 6 = 8
Ngoài sách giáo khoa, học sinh có thể tham khảo thêm các tài liệu sau để hỗ trợ giải bài tập 37 trang 125 Toán 7 tập 2:
Bài tập 37 trang 125 Toán 7 tập 2 là một bài tập quan trọng giúp học sinh củng cố kiến thức về biểu thức đại số. Bằng cách nắm vững các quy tắc và áp dụng các bước giải đúng, học sinh có thể giải quyết bài tập này một cách hiệu quả và tự tin hơn trong quá trình học tập. Giaitoan.edu.vn luôn đồng hành cùng các em học sinh trên con đường chinh phục môn Toán.