Bài tập 40 trang 125 Toán 7 tập 2 thuộc chương trình đại số, tập trung vào các kiến thức về biểu thức đại số và các phép toán trên biểu thức. Bài tập này thường yêu cầu học sinh vận dụng các quy tắc, tính chất đã học để đơn giản hóa biểu thức, tìm giá trị của biểu thức hoặc chứng minh đẳng thức.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho Bài tập 40 trang 125, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Giải bài tập Cho tam giác ABC cân tại A, hai đường cao BE và CF cắt nhau tại H. Tia AH cắt A, đường cao BE và CF cắt nhau tại H. Tia AH cắt BC tại I. Chứng minh I là trung điểm của BC.
Đề bài
Cho tam giác ABC cân tại A, hai đường cao BE và CF cắt nhau tại H. Tia AH cắt A, đường cao BE và CF cắt nhau tại H. Tia AH cắt BC tại I. Chứng minh I là trung điểm của BC.
Lời giải chi tiết
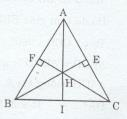
∆ABC có hai đường cao BE và CF cắt nhau tại H (gt)
=> H là trực tâm của ∆ABC.
Mà AI đi qua H (gt). Nên AI là đường cao của ∆ABC.
∆ABC cân tại A có AI là đường cao.
Do đó AI là đường trung tuyến.
Vậy I là trung điểm của BC.
Bài tập 40 trang 125 Toán 7 tập 2 là một phần quan trọng trong chương trình học Toán 7, tập trung vào việc củng cố kiến thức về biểu thức đại số. Để giải quyết bài tập này một cách hiệu quả, học sinh cần nắm vững các quy tắc về thứ tự thực hiện các phép toán, các tính chất giao hoán, kết hợp, phân phối của phép nhân đối với phép cộng và phép trừ.
Bài tập 40 thường bao gồm các dạng bài tập sau:
Ví dụ 1: Tính giá trị của biểu thức 3x + 2y khi x = 2 và y = -1.
Giải:
Thay x = 2 và y = -1 vào biểu thức, ta có:
3x + 2y = 3 * 2 + 2 * (-1) = 6 - 2 = 4
Vậy, giá trị của biểu thức 3x + 2y khi x = 2 và y = -1 là 4.
Ví dụ 2: Rút gọn biểu thức 2(x + 3) - 5x.
Giải:
2(x + 3) - 5x = 2x + 6 - 5x = (2x - 5x) + 6 = -3x + 6
Vậy, biểu thức 2(x + 3) - 5x được rút gọn thành -3x + 6.
Ngoài sách giáo khoa, bạn có thể tham khảo thêm các tài liệu sau để học tốt Toán 7:
Bài tập 40 trang 125 Toán 7 tập 2 là một bài tập quan trọng giúp học sinh củng cố kiến thức về biểu thức đại số. Bằng cách nắm vững các quy tắc, tính chất và thực hành thường xuyên, bạn có thể giải quyết bài tập này một cách hiệu quả và đạt kết quả tốt trong môn Toán.