Giaitoan.edu.vn xin giới thiệu lời giải chi tiết Bài tập 20 trang 117 Toán 7 tập 1. Bài tập này thuộc chương trình học Toán 7, tập trung vào việc rèn luyện kỹ năng giải toán về các phép toán với số hữu tỉ.
Chúng tôi cung cấp các bước giải dễ hiểu, kèm theo giải thích rõ ràng để giúp học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Giải bài tập Vẽ một đường thẳng cắt hai đường thẳng sao cho trong các góc tạo thành có một cặp góc so le trong bằng nhau. Đặt tên cho các góc đó.
Đề bài
Vẽ một đường thẳng cắt hai đường thẳng sao cho trong các góc tạo thành có một cặp góc so le trong bằng nhau. Đặt tên cho các góc đó.
a) Vì sao cặp góc so le trong còn lại cũng bằng nhau ?
b) Vì sao các cặp góc đồng vị cũng bằng nhau ?
c) Vì sao các cặp góc trong cùng phía bù nhau ?
Lời giải chi tiết
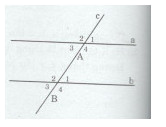
Đường thẳng c cắt hai đường thẳng a và b tạo thành hai góc A4 và B2 so le trong bằng nhau.
a)Ta có: \(\widehat {{A_4}} + \widehat {{A_3}} = \widehat {{B_1}} + \widehat {{B_2}}\)
(=1800 hai cặp góc kề bù)
Mà \(\widehat {{A_4}} = \widehat {{B_2}}\) (giả thiết) nên \(\widehat {{A_3}} = \widehat {{B_1}}\)
Vậy các cặp góc so le trong còn lại cũng bằng nhau.
b) Ta có: \(\widehat {{A_3}} = \widehat {{B_1}}\) (chứng minh câu a) và \(\widehat {{A_1}} = \widehat {{A_3}}\) (hai góc đối đỉnh) \( \Rightarrow \widehat {{A_1}} = \widehat {{B_1}}\)
\(\widehat {{A_3}} = \widehat {{B_1}}\) (chứng minh ở câu a) và \(\widehat {{B_2}} = \widehat {{B_3}}\) (hai góc đối đỉnh) \( \Rightarrow \widehat {{A_3}} = \widehat {{B_3}}\)
Ta có: \(\widehat {{A_4}} = \widehat {{B_2}}\) (hai góc sole trong) và \(\widehat {{B_2}} = \widehat {{B_4}}\) (hai góc đối đỉnh) \( \Rightarrow \widehat {{A_4}} = \widehat {{B_4}}\)
Ta có: \(\widehat {{A_4}} = \widehat {{B_2}}\) (hai góc sole trong) và \(\widehat {{A_2}} = \widehat {{A_4}}\) (hai góc đối đỉnh) \( \Rightarrow \widehat {{A_2}} = \widehat {{B_2}}\)
Vậy các cặp góc đồng vị cũng bằng nhau.
c) Ta có: \(\widehat {{A_1}} + \widehat {{A_4}} = {180^0}\) (hai góc kề bù) và \(\widehat {{A_1}} = \widehat {{B_1}}\) (chứng minh câu b)
Suy ra: \(\widehat {{B_1}} + \widehat {{A_4}} = {180^0}\)
Ta có: \(\widehat {{A_2}} + \widehat {{A_3}} = {180^0}\) (hai góc kề bù) và \(\widehat {{A_2}} = \widehat {{B_2}}\) (chứng minh câu b)
Suy ra: \(\widehat {{B_2}} + \widehat {{A_3}} = {180^0}\)
Vậy các cặp góc trong cùng phía bù nhau.
Bài tập 20 trang 117 Toán 7 tập 1 là một phần quan trọng trong chương trình học Toán 7, tập trung vào việc củng cố kiến thức về các phép toán với số hữu tỉ. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản như số hữu tỉ, phép cộng, trừ, nhân, chia số hữu tỉ, và các quy tắc ưu tiên thực hiện các phép toán.
Trước khi bắt đầu giải bài tập, học sinh cần đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Điều này giúp học sinh tránh được những sai sót không đáng có và tìm ra phương pháp giải phù hợp.
Dưới đây là lời giải chi tiết cho Bài tập 20 trang 117 Toán 7 tập 1:
Bài tập 20 trang 117 Toán 7 tập 1 không chỉ giúp học sinh củng cố kiến thức về các phép toán với số hữu tỉ mà còn rèn luyện kỹ năng giải toán, tư duy logic và khả năng áp dụng kiến thức vào thực tế. Những kỹ năng này rất quan trọng trong quá trình học tập và làm việc sau này.
Để hiểu sâu hơn về các phép toán với số hữu tỉ, học sinh có thể tham khảo thêm các tài liệu học tập khác, xem các video hướng dẫn trên internet, hoặc tìm kiếm sự giúp đỡ của giáo viên và bạn bè. Việc tự học và tìm tòi kiến thức mới là một trong những yếu tố quan trọng để đạt được thành công trong học tập.
Để luyện tập thêm, học sinh có thể giải các bài tập tương tự trong sách giáo khoa Toán 7 tập 1 hoặc tìm kiếm trên các trang web học toán online. Việc luyện tập thường xuyên sẽ giúp học sinh nắm vững kiến thức và tự tin giải các bài tập khó hơn.
Bài tập 20 trang 117 Toán 7 tập 1 là một bài tập quan trọng giúp học sinh củng cố kiến thức về các phép toán với số hữu tỉ. Hy vọng rằng với lời giải chi tiết và những lưu ý trên, học sinh sẽ giải bài tập này một cách dễ dàng và hiệu quả.