Chào mừng bạn đến với chuyên mục giải bài tập Toán 7 tập 2 của giaitoan.edu.vn. Bài viết này sẽ cung cấp lời giải chi tiết và dễ hiểu cho Bài tập 7 trang 120, giúp các em học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng cao, hỗ trợ tối đa cho quá trình học tập của các em. Hãy cùng bắt đầu với bài tập 7 trang 120 Toán 7 tập 2 ngay bây giờ!
Giải bài tập Chứng minh rằng : Trong một tam giác vuông đường trung tuyến ứng với cạnh huyền thì bằng nửa cạnh huyền.
Đề bài
Chứng minh rằng : Trong một tam giác vuông đường trung tuyến ứng với cạnh huyền thì bằng nửa cạnh huyền.
Lời giải chi tiết
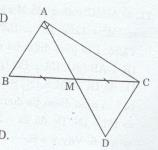
Trên tia đối của tia MA lấy điểm D sao cho MA = MD
Xét ∆ABM và ∆MCD ta có:
BM = MC (M là trung điểm của BC)
AM = MD (cách vẽ)
Và \(\widehat {AMB} = \widehat {CMD}\) (hai góc đối đỉnh)
Do đó: ∆ABM = ∆DCM (c.g.c) \( \Rightarrow \widehat {BAM} = \widehat {MDC}\)
Mà \(\widehat {BAM}\) và\(\widehat {MDC}\) ở vị trí so le trong. Do đó AB // CD.
Ta có AB // CD, \(AB \bot AC\) (∆ABC vuông tại A) \( \Rightarrow CD \bot AC \Rightarrow \widehat {ACD} = 90^\circ\)
Xét ∆ACD và ∆ABC ta có: CD = AB (vì ∆DCM = ABM)
\(\widehat {ACD} = \widehat {BAC}( = 90^\circ )\)
AC là cạnh chung
Do đó: ∆ACD = ∆CAB (c.g.c) => AD = BC
Mà \(AM = {1 \over 2}AD(MA = MD)\). Do đó \(AM = {1 \over 2}BC.\)
Bài tập 7 trang 120 Toán 7 tập 2 thuộc chương trình học Toán 7 tập 2, tập trung vào việc vận dụng các kiến thức đã học về biểu thức đại số, các phép toán trên đa thức để giải quyết các bài toán cụ thể. Dưới đây là lời giải chi tiết cho từng phần của bài tập, kèm theo hướng dẫn giải để các em có thể tự học và rèn luyện.
Bài tập 7a yêu cầu chúng ta thực hiện các phép tính cộng, trừ đa thức. Để giải bài tập này, các em cần nắm vững quy tắc cộng, trừ các đơn thức đồng dạng và các tính chất của phép cộng, trừ.
Bài tập 7b yêu cầu chúng ta thực hiện các phép nhân, chia đa thức. Để giải bài tập này, các em cần nắm vững quy tắc nhân, chia các đơn thức và các tính chất của phép nhân, chia.
Bài tập 7c yêu cầu chúng ta rút gọn biểu thức đại số. Để giải bài tập này, các em cần kết hợp các quy tắc cộng, trừ, nhân, chia đa thức và các tính chất của phép toán.
Ví dụ: Rút gọn biểu thức A = (2x + 3y) * (x - y) - (x + y)2
Hy vọng với lời giải chi tiết và hướng dẫn giải trên, các em học sinh đã có thể tự tin giải quyết Bài tập 7 trang 120 Toán 7 tập 2. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!