Chào mừng bạn đến với bài giải chi tiết Bài 7 trang 171 Toán 7 tập 1 tại giaitoan.edu.vn. Chúng tôi cung cấp đáp án chính xác và lời giải dễ hiểu, giúp bạn nắm vững kiến thức và tự tin giải các bài tập tương tự.
Bài 7 thuộc chương trình học Toán 7 tập 1, tập trung vào việc rèn luyện kỹ năng giải toán về các biểu thức đại số và ứng dụng thực tế. Hãy cùng chúng tôi khám phá cách giải bài tập này một cách hiệu quả nhất.
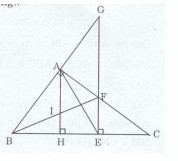
Giải bài tập Cho tam giác ABC vuông tại A (AB < AC). Trên cạnh BC lấy điểm E sao cho BE = BA. Đường thẳng qua E vuông góc BE = BA. Đường thẳng qua E vuông góc với BC cắt AC ở F và cắt AB ở G.
Đề bài
Cho tam giác ABC vuông tại A (AB < AC). Trên cạnh BC lấy điểm E sao cho BE = BA. Đường thẳng qua E vuông góc BE = BA. Đường thẳng qua E vuông góc với BC cắt AC ở F và cắt AB ở G.
a) Chứng minh rằng tam giác AEF cân.
b) Chứng minh rằng AC = GE.
c) Kẻ \(AH \bot BC(H \in BC).\) Gọi I là giao điểm của AH và BF. Chứng minh rằng tam giác AIF cân.
Lời giải chi tiết
a)Xét tam giác ABF vuông tại A và tam giác EBF vuông tại E có:
BF là cạnh chung.
BA = BE (gt)
Do đó \(\Delta ABF = \Delta EBF\) (cạnh huyền - cạnh góc vuông)
=>AF = EF => tam giác AEF cân tại F.
b) Xét tam giác ABC và EBG có:
\(\widehat {BAC} = \widehat {BEG}( = {90^0})\)
BA = BE (gt)
\(\widehat {ABC}\) là góc chung.
Do đó: \(\Delta ABC = \Delta EBG(g.c.g) \Rightarrow AC = GE.\)
c) Ta có: \(\eqalign{ & AH \bot BC(gt) \cr & EF \bot BC(gt) \cr} \)
\(\Rightarrow AH = EF \Rightarrow \widehat {AIF} = \widehat {BFE}\) (so le trong)
Mà \(\widehat {AFI} = \widehat {BFE}(\Delta ABF = \Delta EBF) \Rightarrow \widehat {AIF} = \widehat {AFI}.\)
Do đó: tam giác AIF cân tại A.
Bài 7 trang 171 Toán 7 tập 1 yêu cầu học sinh vận dụng kiến thức về các phép toán với số hữu tỉ, các tính chất của phép cộng, phép trừ, phép nhân, phép chia để giải các bài toán cụ thể. Bài tập này không chỉ giúp củng cố lý thuyết mà còn rèn luyện kỹ năng tính toán và tư duy logic.
Bài 7 thường bao gồm các dạng bài tập sau:
Để giải Bài 7 trang 171 Toán 7 tập 1 một cách hiệu quả, bạn có thể tham khảo các bước sau:
Ví dụ 1: Tính giá trị của biểu thức sau: A = (1/2 + 1/3) * 6/5
Giải:
A = (3/6 + 2/6) * 6/5
A = 5/6 * 6/5
A = 1
Ví dụ 2: Tìm x biết: x + 2/5 = 1/2
Giải:
x = 1/2 - 2/5
x = 5/10 - 4/10
x = 1/10
Ngoài sách giáo khoa, bạn có thể tham khảo thêm các tài liệu sau:
Bài 7 trang 171 Toán 7 tập 1 là một bài tập quan trọng giúp học sinh củng cố kiến thức về số hữu tỉ và các phép toán. Bằng cách nắm vững các kiến thức lý thuyết và thực hành giải các bài tập tương tự, bạn sẽ tự tin hơn trong việc học Toán 7.
| Dạng bài tập | Phương pháp giải |
|---|---|
| Tính toán biểu thức | Thực hiện các phép toán theo thứ tự ưu tiên |
| Tìm x | Biến đổi phương trình để tìm x |
| Bài toán ứng dụng | Phân tích đề bài và xây dựng phương trình |
| Nguồn: giaitoan.edu.vn | |