Chào mừng các em học sinh đến với lời giải Bài tập 4 trang 127 Toán 7 tập 2. Bài tập này thuộc chương trình học Toán 7, tập trung vào việc rèn luyện kỹ năng giải toán về các phép toán với số hữu tỉ.
Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập tương tự.
Giải bài tập Cho tam giác ABC cân tại A
Đề bài
Cho tam giác ABC cân tại A \(\left( {\widehat A < {{90}^o}} \right)\). Hai đường cao BE, CF cắt nhau tại H.
a) Chứng minh rằng \(\Delta BEC = \Delta CFB\)
b) Chứng minh rằng \(\Delta AHF = \Delta AHE\)
c) Gọi I là trung điểm của BC. Chứng minh rằng A, H, I thẳng hàng.
Lời giải chi tiết
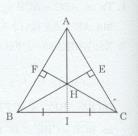
a) Xét ∆BEC (\(\widehat E = 90^\circ\)) và ∆CFB (\(\widehat F = 90^\circ\)) ta có:
BC (cạnh chung) và \(\widehat {BCE} = \widehat {CBF}\) (∆ABC cân tại A).
Do đó: ∆BEC = ∆CFB (cạnh huyền – góc nhọn).
b) Ta có: AB = AC (∆ABC cân tại A).
BF = CE (∆CBF = ∆BEC).
=> AB – BF = AC – CE => AF = AE.
Xét ∆AHF (\(\widehat F = 90^\circ\)) và ∆AHE (\(\widehat E = 90^\circ\)) ta có:
AH (cạnh chung) và AF = AE.
Do đó: ∆AHF = ∆AHE (cạnh huyền – cạnh góc vuông).
c) ∆ABC có hai đường cao BE và CF cắt nhau tại H (gt)
=> H là trực tâm của ∆ABC => AH là đường cao của ∆ABC
Mà ∆ABC cân tại A. Nên AH cũng là đường trung tuyến của ∆ABC
Lại có I là trung điểm của BC (gt). Nên A, H, I thẳng hàng.
Bài tập 4 trang 127 Toán 7 tập 2 yêu cầu học sinh vận dụng kiến thức về các phép toán với số hữu tỉ để thực hiện các phép tính cộng, trừ, nhân, chia. Để giải bài tập này một cách hiệu quả, các em cần nắm vững các quy tắc sau:
Trước khi bắt tay vào giải bài tập, các em cần đọc kỹ đề bài, xác định rõ yêu cầu của bài toán. Ví dụ, bài tập có thể yêu cầu tính giá trị của một biểu thức, tìm x, hoặc giải một bài toán thực tế liên quan đến số hữu tỉ.
Dưới đây là lời giải chi tiết cho từng phần của Bài tập 4 trang 127 Toán 7 tập 2. Các em có thể tham khảo để hiểu rõ cách giải và áp dụng vào các bài tập tương tự.
Ví dụ 1: Tính (-1/2) + (3/4)
Giải:
Vậy, (-1/2) + (3/4) = 1/4
Ví dụ 2: Tính (2/3) * (-5/7)
Giải:
(2/3) * (-5/7) = (2 * -5) / (3 * 7) = -10/21
Vậy, (2/3) * (-5/7) = -10/21
Để củng cố kiến thức về các phép toán với số hữu tỉ, các em có thể tham khảo thêm các bài tập tương tự trong sách giáo khoa và các tài liệu tham khảo khác. Ngoài ra, các em cũng có thể luyện tập thêm trên các trang web học toán online để nâng cao kỹ năng giải toán.
Kiến thức về số hữu tỉ có ứng dụng rất lớn trong thực tế, ví dụ như trong việc tính toán tiền bạc, đo lường, và giải các bài toán liên quan đến tỷ lệ, phần trăm. Việc nắm vững kiến thức này sẽ giúp các em tự tin hơn trong cuộc sống và học tập.
Bài tập 4 trang 127 Toán 7 tập 2 là một bài tập quan trọng giúp các em rèn luyện kỹ năng giải toán về các phép toán với số hữu tỉ. Hy vọng với lời giải chi tiết và phương pháp giải được trình bày ở trên, các em sẽ tự tin hơn trong việc giải bài tập này và các bài tập tương tự.
Chúc các em học tốt!