Chào mừng bạn đến với bài giải Bài 2 trang 175 Toán 7 Tập 1 trên giaitoan.edu.vn. Bài viết này cung cấp lời giải chi tiết, từng bước, giúp bạn hiểu rõ cách giải các bài toán trong bài học.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng, hỗ trợ bạn học toán một cách hiệu quả nhất.
Giải bài tập Cho tam giác ABC cân tại A.
Đề bài
Cho tam giác ABC cân tại A. Kẻ \(BM \bot AC(M \in AC),CN \bot AB(N \in AB).\)
a) Chứng minh rằng \(\Delta BMC = \Delta CNB.\)
b) Gọi I là giao điểm của BM với CN. Chứng minh rằng \(\Delta AIN = \Delta AIM.\)
c) AI cắt BC tại H, biết AB = 10 cm, BC = 12 cm. Tính AH.
Lời giải chi tiết
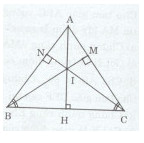
a)Xét tam giác BMC vuông tại M và CNB vuông tại N có:
BC là cạnh chung.
\(\widehat {MCB} = \widehat {NBC}\) (tam giác ABC cân tại A)
Do đó: \(\Delta BMC = \Delta CVB\) (cạnh huyền - góc nhọn)
b) Ta có: AN + NB = AB và AM + MC = AC.
Mà AB = AC (tam giác ABC cân tại A)
Nên AN + NB = AM + MC.
Vì BN = MC \((\Delta BMC = \Delta CNB)\)
Nên AN = AM.
Xét tam giác ANI vuông tại N và AMI vuông tại M ta có:
AI là cạnh chung.
AN = AM (chứng minh trên)
Do đó: \(\Delta ANI = \Delta AMI\) (cạnh huyền - cạnh góc vuông).
c)Xét tam giác ABH và ACH ta có:
AB = AC (tam giác ACB cân tại A)
AH là cạnh chung.
\(\widehat {BAH} = \widehat {CAH}(\Delta ANI = \Delta AMI)\)
Do đó: \(\Delta ABH = \Delta ACH(c.g.c) \Rightarrow BH = CH;\widehat {AHB} = \widehat {AHC}\)
Do đó: \(BH = CH = {{BC} \over 2} = {{12} \over 2} = 6(cm).\)
\(\widehat {AHB} + \widehat {AHC} = {180^0}\) (hai góc kề bù)
Nên \(\widehat {AHB} + \widehat {AHB} = {180^0}(\widehat {AHB} = \widehat {AHC}) \Rightarrow 2\widehat {AHB} = {180^0} \Rightarrow \widehat {AHB} = {90^0} \Rightarrow AH \bot BC\)
Tam giác ABH vuông tại H \(\Rightarrow A{H^2} + B{H^2} = A{B^2}\) (định lí Pythagore).
Do đó: \(A{H^2} = A{B^2} - B{H^2} = {10^2} - {6^2} = 100 - 36 = 64.\)
Mà AH > 0. Vậy \(AH = \sqrt {64} = 8(cm).\)
Bài 2 trang 175 Toán 7 Tập 1 thuộc chương trình học Toán 7, tập trung vào việc vận dụng các kiến thức đã học về biểu thức đại số, các phép toán với số hữu tỉ, và các tính chất của phép cộng, trừ, nhân, chia để giải quyết các bài toán cụ thể. Việc nắm vững kiến thức nền tảng là yếu tố then chốt để giải quyết thành công bài tập này.
Bài 2 thường bao gồm các dạng bài tập sau:
Để giải quyết Bài 2 trang 175 Toán 7 Tập 1 một cách hiệu quả, bạn có thể tham khảo các bước sau:
Ví dụ: Tính giá trị của biểu thức 3x + 2y khi x = 2 và y = -1.
Giải:
Thay x = 2 và y = -1 vào biểu thức, ta có:
3x + 2y = 3(2) + 2(-1) = 6 - 2 = 4
Vậy, giá trị của biểu thức 3x + 2y khi x = 2 và y = -1 là 4.
Để hỗ trợ quá trình học tập và giải bài tập, bạn có thể tham khảo các tài liệu sau:
Bài 2 trang 175 Toán 7 Tập 1 là một bài tập quan trọng giúp học sinh củng cố kiến thức về biểu thức đại số và các phép toán với số hữu tỉ. Bằng cách nắm vững kiến thức nền tảng, áp dụng các bước giải đúng đắn, và luyện tập thường xuyên, bạn có thể giải quyết thành công bài tập này và đạt kết quả tốt trong môn Toán.
Hy vọng rằng bài viết này đã cung cấp cho bạn những thông tin hữu ích và giúp bạn hiểu rõ hơn về Bài 2 trang 175 Toán 7 Tập 1. Chúc bạn học tập tốt!