Bài tập 35 trang 124 Toán 7 tập 2 thuộc chương trình đại số lớp 7, tập trung vào các kiến thức về biểu thức đại số và các phép toán trên biểu thức. Bài tập này giúp học sinh rèn luyện kỹ năng vận dụng kiến thức đã học vào giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho từng bài tập, giúp học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Giải bài tập Cho tam giác ABC cân tại A có góc A nhọn. Tia phân giác của góc BAC cắt BC tại M.
Đề bài
Cho tam giác ABC cân tại A có góc A nhọn. Tia phân giác của góc BAC cắt BC tại M.
a) Chứng minh rằng \(\Delta AMB = \Delta AMC\)
b) Vẽ trung tuyến CE của tam giác ABC cắt AM tại G. Chứng minh G là trọng tâm của tam giác ABC.
c) Biết độ dài BM = 12 cm, AB = 20 cm. Tính độ dài AG.
d) Qua M kẻ đường thẳng song song với AB cắt AC tại N. Chứng minh ba điểm A, G, N thẳng hàng.
Lời giải chi tiết
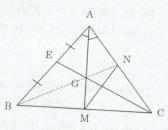
a) Xét ∆AMB và ∆AMC ta có:
AM (cạnh chung)
\(\widehat {BAM} = \widehat {MAC}\) (AM là tia phân giác của \(\widehat {BAC}\))
Và AB = AC (∆ABC cân tại A)
Do đó: ∆AMB = ∆AMC (c.g.c).
b) ∆ABC cân tại A có AM là đường phân giác (gt)
=> AM là đường trung tuyến của ∆ABC.
Mà CE là đường trung tuyến của ∆ABC (gt) và AM cắt CE tại G (gt)
Nên G là trọng tâm của ∆ABC.
c) ∆ABC cân tại A có AM là đường phân giác (gt)
=> AM là đường cao của ∆ABC \( \Rightarrow AM \bot BC\) tại M => ∆ABM vuông tại M
=> AM2 + BM2 = AB2 (định lí Pythagore)
=> AM2 + 122 = 202 => AM2 = 256 = 162 => AM = 16 (cm)
∆ABC có AM là đường trung tuyến (câu b) và G là trọng tâm (câu b)
\( \Rightarrow AG = {2 \over 3}AM = {2 \over 3}.16 = {{32} \over 3}(cm).\)
d) Ta có: \(\widehat {ABC} = \widehat {NCM}\) (∆ABC cân tại A)
\(\widehat {ABC} = \widehat {NMC}\) (hai góc đồng vị và MN // AB)
Do đó \(\widehat {NCM} = \widehat {NMC}\) => ∆NCM cân tại N => NM = NC (1)
Mặt khác: \(\widehat {BAM} = \widehat {AMN}\) (hai góc so le trong và AB // MN)
\(\widehat {BAM} = \widehat {MAN}\) (AM là tia phân giác của \(\widehat {BAC}\))
\( \Rightarrow \widehat {AMN} = \widehat {MAN}\) => ∆AMN cân tại N => NM = NA (2)
Từ (1) và (2) suy ra NC = NA
=> N là trung điểm của AC (\(N \in AC\)) => BN là đường trung tuyến của ∆ABC
Mà G là trọng tâm của ∆ABC (câu b). Nên BN đi qua G
Vậy B, G, N thẳng hàng.
Bài tập 35 trang 124 Toán 7 tập 2 là một phần quan trọng trong chương trình học Toán lớp 7, tập trung vào việc củng cố kiến thức về biểu thức đại số và các phép toán cơ bản. Để giúp học sinh hiểu rõ hơn và tự tin giải quyết các bài tập, giaitoan.edu.vn xin giới thiệu lời giải chi tiết và hướng dẫn từng bước.
Bài tập 35 bao gồm các câu hỏi liên quan đến việc thu gọn biểu thức đại số, tìm giá trị của biểu thức khi biết giá trị của biến, và thực hiện các phép toán cộng, trừ, nhân, chia đa thức. Các bài tập được thiết kế để học sinh vận dụng các kiến thức đã học vào giải quyết các tình huống thực tế.
Để giải bài tập 35 trang 124 Toán 7 tập 2, học sinh cần nắm vững các kiến thức sau:
Dưới đây là lời giải chi tiết cho từng câu hỏi trong bài tập 35:
...
...
...
Để giải bài tập 35 trang 124 Toán 7 tập 2 một cách hiệu quả, học sinh có thể áp dụng các mẹo sau:
Bài tập 35 trang 124 Toán 7 tập 2 có ứng dụng rộng rãi trong thực tế, giúp học sinh:
Bài tập 35 trang 124 Toán 7 tập 2 là một bài tập quan trọng giúp học sinh củng cố kiến thức về biểu thức đại số và các phép toán cơ bản. Hy vọng với lời giải chi tiết và hướng dẫn của giaitoan.edu.vn, học sinh sẽ tự tin giải quyết các bài tập tương tự và đạt kết quả tốt trong môn Toán.
| Bài tập | Lời giải |
|---|---|
| Câu a | ... |
| Câu b | ... |
| Câu c | ... |