Chào mừng bạn đến với bài giải chi tiết Bài 5 trang 175 Tài liệu dạy – học Toán 7 tập 1 tại giaitoan.edu.vn. Bài viết này cung cấp lời giải đầy đủ, dễ hiểu, giúp các em học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng cao, hỗ trợ tối đa cho quá trình học tập của các em. Hãy cùng bắt đầu với bài giải chi tiết ngay sau đây!
Giải bài tập Cho tam giác ABC cân tại A. Trên cạnh BC lần lượt lấy hai điểm M và N sao cho MN = MN = NC. Gọi H là trung điểm của BC.
Đề bài
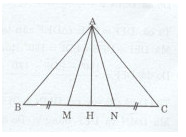
Cho tam giác ABC cân tại A. Trên cạnh BC lần lượt lấy hai điểm M và N sao cho MN = MN = NC. Gọi H là trung điểm của BC.
a) Chứng minh rằng AM = AN.
b) Chứng minh rằng \(AH \bot BC.\)
c) Cho biết AB = 5 cm, BC = 6 cm. Tính AM.
Lời giải chi tiết
a)Xét tam giác ABM và CAN ta có:
AB = AC (tam giác ABC cân tại A)
\(\widehat {ABM} = \widehat {ACN}(\Delta ABC\) cân tại A)
BM = CN (giả thiết)
Do đó: \(\Delta ABM = \Delta ACN(c.g.c) \Rightarrow AM = AN.\)
b)Xét hai tam giác ABH và ACH ta có:
AB = AC (tam giác ABC cân tại A)
BH = CH (H là trung điểm BC)
AH là cạnh chung.
Do đó: \(\Delta ABH = \Delta ACH(c.c.c) \Rightarrow \widehat {AHB} = \widehat {AHC}.\)
Mà \(\widehat {AHB} + \widehat {AHC} = {180^0}\) (hai góc kề bù)
Nên \(\widehat {AHB} + \widehat {AHB} = {180^0} \Rightarrow 2\widehat {AHB} = {180^0} \Rightarrow \widehat {AHB} = {90^0}.\) Vậy \(AH \bot BC.\)
c) Ta có: \(\eqalign{ & BH = HC = {{BC} \over 2} = {6 \over 2} = 3cm \cr & BM = MN = NC = {{BC} \over 2} = {6 \over 3} = 2cm \cr & BM + MH = BH \Rightarrow MH = BH - BM = 3 - 2 = 1(cm). \cr} \)
Tam giác ABH vuông tại H \(\Rightarrow A{B^2} = A{H^2} + B{H^2}\) (định lí Pythagore)
Do đó: \(A{H^2} = A{B^2} - B{H^2} = {5^2} - {3^2} = 16,AH > 0\) Vậy \(AH = \sqrt {16} = 4(cm).\)
Tam giác AMH vuông tại H \(\Rightarrow A{M^2} = A{H^2} + M{H^2}\) (định lí Pythagore)
Do đó: \(A{M^2} = {4^2} + {1^2} = 16 + 1 = 17\)
Mà AM > 0. Vậy \(AM = \sqrt {17} (cm).\)
Bài 5 trang 175 thuộc chương trình Toán 7 tập 1, tập trung vào việc vận dụng các kiến thức về số hữu tỉ, phép cộng, trừ, nhân, chia số hữu tỉ để giải quyết các bài toán thực tế. Bài tập này thường yêu cầu học sinh phải hiểu rõ các quy tắc, tính chất của các phép toán và biết cách áp dụng chúng một cách linh hoạt.
Bài 5 thường bao gồm các dạng bài tập sau:
Để giải Bài 5 trang 175 một cách hiệu quả, học sinh cần:
Ví dụ 1: Tính giá trị của biểu thức sau: A = (1/2 + 1/3) * 2/5
Giải:
A = (3/6 + 2/6) * 2/5
A = 5/6 * 2/5
A = 10/30 = 1/3
Ví dụ 2: Một cửa hàng có 200 kg gạo. Ngày đầu bán được 1/4 số gạo, ngày thứ hai bán được 2/5 số gạo còn lại. Hỏi sau hai ngày, cửa hàng còn lại bao nhiêu kg gạo?
Giải:
Số gạo bán được ngày đầu là: 200 * 1/4 = 50 kg
Số gạo còn lại sau ngày đầu là: 200 - 50 = 150 kg
Số gạo bán được ngày thứ hai là: 150 * 2/5 = 60 kg
Số gạo còn lại sau hai ngày là: 150 - 60 = 90 kg
Để củng cố kiến thức và rèn luyện kỹ năng giải toán, học sinh có thể tự giải thêm các bài tập tương tự trong sách giáo khoa và các tài liệu tham khảo khác. Ngoài ra, các em cũng có thể tham gia các diễn đàn, nhóm học tập trực tuyến để trao đổi kinh nghiệm và học hỏi lẫn nhau.
Kiến thức về số hữu tỉ là nền tảng quan trọng cho việc học tập các môn Toán ở các lớp trên. Việc nắm vững các khái niệm, tính chất và quy tắc của số hữu tỉ sẽ giúp học sinh giải quyết các bài toán phức tạp một cách dễ dàng và hiệu quả hơn. Đồng thời, kiến thức này cũng có ứng dụng rộng rãi trong thực tế, giúp học sinh hiểu rõ hơn về thế giới xung quanh.
giaitoan.edu.vn là một website học toán online uy tín, cung cấp đầy đủ các tài liệu học tập, bài giải chi tiết và các bài tập luyện tập cho học sinh các cấp. Với đội ngũ giáo viên giàu kinh nghiệm và phương pháp giảng dạy hiện đại, chúng tôi cam kết mang đến cho học sinh những trải nghiệm học tập tốt nhất.
Hãy truy cập giaitoan.edu.vn ngay hôm nay để khám phá thêm nhiều tài liệu học tập hữu ích và nâng cao kiến thức Toán học của bạn!