Bài tập 9 trang 157 thuộc chương trình Toán 7 tập 1, là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về các phép toán với số hữu tỉ. Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và tự tin giải bài tập.
Chúng tôi không chỉ cung cấp đáp án mà còn phân tích phương pháp giải, giúp học sinh hiểu rõ bản chất của bài toán.
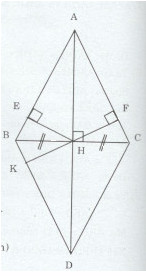
Giải bài tập Cho tam giác ABC có AB = AC, phân giác của góc A cắt BC tại H.
Đề bài
Cho tam giác ABC có AB = AC, phân giác của góc A cắt BC tại H.
a) Chứng minh rằng \(\Delta AHB = \Delta AHC\)
b) Chứng minh rằng AH vuông góc với BC.
c) Kẻ \(HE \bot AB(E \in AB),HF \bot AC(F \in AC).\) Chứng minh rằng \(\Delta HEB = \Delta HFC\)
d) Trên tia đối của tia HA ta lấy điểm D sao cho H là trung điểm của AD. Chứng minh rằng \(FH \bot BD\)
Lời giải chi tiết
a)Xét tam giác AHB và AHC có:
AB = AC (giả thiết)
\(\widehat {BAH} = \widehat {CAH}\) (AH là tia phân giác của góc BAC)
AH là cạnh chung.
Do đó: \(\Delta AHB = \Delta AHC(c.g.c)\)
b) Ta có: \(\Delta AHB = \Delta AHC\) (chứng minh câu a)
Suy ra: \(\widehat {AHB} = \widehat {AHC};\widehat {ABH} = \widehat {ACH}\)
Mà \(\widehat {AHB} + \widehat {AHC} = {180^0}\) (kề bù)
Nên \(\eqalign{ & \widehat {AHC} + \widehat {AHC} = {180^0} \Rightarrow 2\widehat {AHC} = {180^0}. \cr & \widehat {AHC} = {90^0} \Rightarrow AH \bot BC \cr} \)
c) Tam giác EBH vuông tại E có: \(\widehat {EBH} + \widehat {EHB} = {90^0}\)
Tam giác FHC vuông tại F có: \(\widehat {FHC} + \widehat {FCH} = {90^0}\)
Mà \(\widehat {EBH} = \widehat {FCH}\) (chứng minh câu b) nên \(\widehat {EHB} = \widehat {FHC.}\)
Xét tam giác HEB và HFC có:
\(\eqalign{ & \widehat {EBH} = \widehat {FCH} \cr & \widehat {EHB} = \widehat {FHC}(cmt) \cr & HB = HC(\Delta AHB = \Delta AHC) \cr} \)
Do đó: \(\Delta HEB = \Delta HFC(g.c.g)\)
d) Xét tam giác AHC và DHB có:
AH = DH (giả thiết)
\(\eqalign{ & HC = HB(\Delta AHB = \Delta AHC) \cr & \widehat {AHC} = \widehat {BHD}( = {90^0}) \cr} \)
Do đó: \(\Delta AHC = \Delta DHB(c.g.c) \Rightarrow \widehat {HAC} = \widehat {HDB}\)
Mà hai góc này ở vị trí so le trong do đó AC // BD.
Mặt khác \(HF \bot AC\) (giả thiết) nên ta có: \(HF \bot BD\)
Bài tập 9 trang 157 Toán 7 tập 1 yêu cầu học sinh thực hiện các phép tính với số hữu tỉ. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các quy tắc về cộng, trừ, nhân, chia số hữu tỉ, cũng như quy tắc chuyển đổi phân số về dạng tối giản.
Phần a của bài tập thường yêu cầu thực hiện một chuỗi các phép tính cộng, trừ, nhân, chia số hữu tỉ. Để giải phần này, học sinh cần thực hiện các phép tính theo đúng thứ tự ưu tiên: trong ngoặc trước, nhân chia trước, cộng trừ sau.
Ví dụ:
Phần b thường yêu cầu học sinh rút gọn một biểu thức chứa các số hữu tỉ. Để rút gọn biểu thức, học sinh cần thực hiện các phép tính trong ngoặc trước, sau đó thực hiện các phép tính nhân, chia, cộng, trừ theo đúng thứ tự ưu tiên.
Ví dụ:
Rút gọn biểu thức: (2/3) * (3/4) + (1/2)
Phần c thường yêu cầu học sinh tìm giá trị của x trong một phương trình chứa các số hữu tỉ. Để giải phương trình, học sinh cần thực hiện các phép biến đổi tương đương để đưa phương trình về dạng x = một số hữu tỉ.
Ví dụ:
Tìm x: x + (1/2) = (3/4)
Bài tập 9 trang 157 Toán 7 tập 1 giúp học sinh:
Học sinh có thể tham khảo thêm các tài liệu sau để hiểu rõ hơn về các phép toán với số hữu tỉ:
Bài tập 9 trang 157 Toán 7 tập 1 là một bài tập quan trọng giúp học sinh củng cố kiến thức và rèn luyện kỹ năng giải toán. Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin giải bài tập và đạt kết quả tốt trong môn Toán.