Chào mừng bạn đến với bài giải chi tiết Bài 19 trang 170 Toán 7 tập 1 tại giaitoan.edu.vn. Bài viết này sẽ cung cấp đáp án chính xác và phương pháp giải bài tập một cách dễ hiểu, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng cao, hỗ trợ tối đa cho học sinh trong việc chinh phục môn Toán.
Giải bài tập Cho tam giác ABC cân tại A.
Đề bài
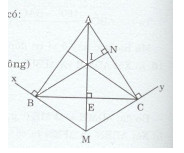
Cho tam giác ABC cân tại A. Kẻ \(Bx \bot AB\) và \(Cy \bot AC.\) Gọi M là giao điểm của Bx và Cy.
a) Chứng minh rằng \(\Delta ABM = \Delta ACM.\)
b) Chứng minh rằng \(AM \bot BC.\)
c) Kẻ \(BN \bot C(N \in AC),\) gọi I là giao điểm của BN với AM. Chứng minh rằng tam giác BIM cân.
d) Chứng minh rằng \(CI \bot AB.\)
Lời giải chi tiết
a)Xét tam giác ABM vuông tại B và tam giác ACM vuông tại C có:
AB = AC (tam giác ABC cân tại A)
AM là cạnh chung.
Do đó: \(\Delta ABM = \Delta ACM\) (cạnh huyền - góc nhọn).
b) Xét tam giác BEM và CEM có:
EM là cạnh chung.
\(\eqalign{ & \widehat {EMB} = \widehat {EMC}(\Delta ABM = \Delta ACM) \cr & BM = CM(\Delta ABM = \Delta ACM) \cr} \)
Do đó: \(\Delta BEM = \Delta CEM(c.g.c) \Rightarrow \widehat {BEM} = \widehat {CEM}\)
Mà \(\widehat {BEM} + \widehat {CEM} = {180^0}\) (hai góc kề bù).
Nên \(\widehat {BEM} + \widehat {BEM} = {180^0} \Rightarrow 2\widehat {BEM} = {180^0} \Rightarrow \widehat {BEM} = {90^0}\)
Vậy \(AM \bot BC.\)
c) Ta có: \(BN \bot AC(gt);MC \bot AC(gt)\)
\(\Rightarrow BN//MC \Rightarrow \widehat {BIM} = \widehat {IMC}\) (hai góc so le trong).
Mà \(\widehat {IMC} = \widehat {BMI}(\Delta ABM = \Delta ACM) \Rightarrow \widehat {BIM} = \widehat {BMI}.\)
Do đó: Tam giác BIM cân tại B.
d) Xét tam giác BIM và CIM ta có:
BM = CM \((\Delta ABM = \Delta ACM)\)
IM là cạnh chung.
\(\widehat {BMI} = \widehat {CMI}(\Delta ABM = \Delta ACM)\)
Do đó: \(\Delta BIM = \Delta CIM(c.g.c) \Rightarrow \widehat {BIM} = \widehat {CIM}.\)
Mà \(\widehat {BIM} = \widehat {BMI}\) (chứng minh trên). Do đó: \(\widehat {CIM} = \widehat {BMI}.\)
Mà hai góc CIM và BMI so le trong. Do đó CI // MB.
Mà \(MB \bot AB(gt) \Rightarrow CI \bot AB.\)
Bài 19 trang 170 Toán 7 tập 1 thuộc chương trình học Toán 7, tập trung vào việc ôn tập chương I: Số hữu tỉ. Bài tập trong bài này giúp học sinh củng cố kiến thức về các phép toán với số hữu tỉ, so sánh số hữu tỉ, và ứng dụng các kiến thức này vào giải quyết các bài toán thực tế.
Bài 19 bao gồm các bài tập đa dạng, từ việc thực hiện các phép tính đơn giản đến việc giải các bài toán có tính ứng dụng cao hơn. Dưới đây là phân tích chi tiết từng bài tập:
Bài tập này yêu cầu học sinh thực hiện các phép cộng, trừ, nhân, chia số hữu tỉ. Để giải bài tập này, học sinh cần nắm vững các quy tắc về phép toán với số hữu tỉ, bao gồm:
Bài tập này yêu cầu học sinh tìm giá trị của x trong các phương trình chứa số hữu tỉ. Để giải bài tập này, học sinh cần áp dụng các quy tắc về giải phương trình, bao gồm:
Bài tập này yêu cầu học sinh so sánh các số hữu tỉ. Để giải bài tập này, học sinh có thể sử dụng các phương pháp sau:
Để giải Bài 19 trang 170 Toán 7 tập 1 một cách hiệu quả, học sinh nên:
Kiến thức về số hữu tỉ và các phép toán với số hữu tỉ có ứng dụng rộng rãi trong đời sống hàng ngày, ví dụ như:
Bài 19 trang 170 Toán 7 tập 1 là một bài tập quan trọng giúp học sinh củng cố kiến thức về số hữu tỉ và các phép toán với số hữu tỉ. Hy vọng rằng với bài giải chi tiết và những lời khuyên trên, các bạn học sinh sẽ tự tin hơn trong việc giải bài tập và đạt kết quả tốt trong môn Toán.
| Bài tập | Nội dung chính |
|---|---|
| Bài 1 | Thực hiện các phép tính với số hữu tỉ |
| Bài 2 | Tìm x trong phương trình chứa số hữu tỉ |
| Bài 3 | So sánh các số hữu tỉ |
| Nguồn: giaitoan.edu.vn | |